Universidade Federal de Santa Maria

Ci. e Nat., Santa Maria v.42, Special Edition: 40 anos, e37, 2020

DOI:10.5902/2179460X40996

ISSN 2179-460X

Received: 07/11/19   Accepted: 13/11/19  Published: 03/09/20

 

 

40 years - anniversary

 

Existence and decay rates for a semilinear dissipative fractional second order evolution equation

 

Ruy Coimbra Charão ^I

Jaqueline Luiza Horbach ^II

 

^I Universidade Federal de Santa Catarina, Florianópolis, Brazil. E-mail: ruy.charao@ufsc.br.

^II Universidade Federal de Santa Catarina, Florianópolis, Brazil. E-mail: jaqueluizah@gmail.com.

 

 

ABSTRACT

In this work we study the existence and uniqueness of solutions and decay rates to the total energy and the L²-norm of solution for a semilinear second order evolution equation with fractional damping term and under effects of a generalized rotational inertia term in the case of plate equation. This system also includes equations of

Boussinesq type that model hydrodynamic problems. We show decay rates depend- ing on the fractional powers of the operators and using an asymptotic expansion of the solution to the linear problem, we prove for some cases depending on the exponents of the operators, the optimality of the decay rates.

Keywords: Plate/Boussinesq type equation; Fractional Laplacians; Generalized rotational inertia; Fractional dissipation; Existence and uniqueness; Decay rates.

 

 

1 INTRODUCTION

We consider in this work the following Cauchy problem associated to plate/Boussinesq type equations with a fractional damping and a generalized fractional rotational inertia term in Rⁿ

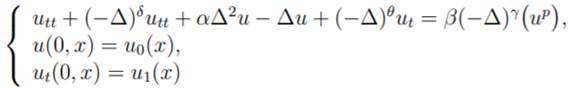
(1)

with u = u(t, x), (t, x) ∈ (0, ∞) × R n , α > 0, β ∈ R, p > 1 integers and u0, u1 are the initial date. The Laplacian power δ , θ and γ are such that 0 ≤ δ ≤ 2, 0 ≤ θ ≤ 2 and 0 ≤ γ ≤ 1.

The function u = u(x, t), for example, in the case δ = 1 and β = 0, describes the transverse displacement of a plate without non-linear effects, but subject to effects of rotational inertia and a fractional dissipation represented by the term (−∆)θut . In the case δ = 0 and β = 0 the linear equation in (1) models the plate displacement without rotational inertial effects.

In the case δ = 2, β 6= 0 and γ = 1 the equation in (1) is a Boussinesq equation of sixth order under dissipative effects to model hydrodynamic problems (see [16], [6]). If δ = α = 0, γ = 1, β 6= 0 and without the dissipative term the equation in (1) is a generalized Boussinesq equation. If the nonlinearity has the form ∆(u 2 ) the equation is called the Boussinesq equation (Bq). With this type of nonlinearity and δ = 1, α = 0 and without the dissipative term, the equation in (1) is called the improved Boussinesq equation (IBq). This same equation with more general linearity as it appears above in (1) is called the IMBq equation (Modified IBq) (see [15]). All these variants of Boussinesq have many physical applications, such as the propagation of longitudinal waves of deformation in an elastic rod in the case of the dimension n = 1, propagation of shallow-water waves. Six-order Boussinesq equation was derived in the study of surface layers of nonlinear plasmas and non-linear chains (see [1], [5]). In Maugin [12], Maugin proposed such a Boussinesq model to model the dynamics of nonlinear networks in elastic crystals.

In the article by Char˜ao-Horbach-Ikehata [7] the authors studied the equation in (1) for the linear case β = 0. In that paper they studied decay rates for the linear problem and showed that the rates are optimal under the conditions 1 2 < θ < min{ 3 2 , δ + 1 2 } and 0 < δ < θ.

In this paper our aim is to show the existence and uniqueness of solution for both the linear problem and the semilinear problem and to get decay rates for the semilinear problem under suitable conditions on the initial data and the fractional exponents of the Laplacian operator. Our results improve several previous works (see [2], [3], [8], [9] [11], [13], [14], [15], [16]).

 

1.1 Basic Results

In this section we introduce some results and technical lemmas that will be used in this paper. Part of these results are known and standard and the proof is not necessary.

The method to prove our results such as properties of the Cauchy Problem (1) includes to apply the Fourier transform to get an equivalent Cauchy problem in Fourier space associated with the problem (1). Thus, we need to define the Fourier Transform of a function as usual.

Definition 1.1: If u ∈ L²(Rⁿ) then we denote for Fu the Fourier Transform of u given by

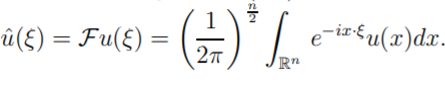
In addition, we denote by F ⁻¹û the inverse Fourier Transform of û given by

For u ∈ H^α (Rⁿ) the operator (−∆)^α is defined via Fourier transform by

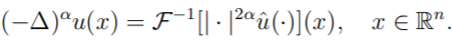
Theorem 1.1 (Plancherel Identity) For all function u ∈ L²(Rⁿ) it holds that ||u|| =||Fu||.

In this work we use the space H^s(Rⁿ) for s ∈ R. The following definition is the equivalent to the usual definition of H^s(Rⁿ).

Definition 1.2: For s ∈ R we define the space

In the case H^s(Rⁿ) with s > 0 we use the following equivalent norm and inner product

In the case H^−s(Rⁿ) with s > 0 we use the norm and inner product given by

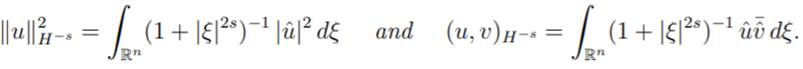
Remark 1.1: When s = 2 we consider the following norm and inner product equivalent to usual

Let consider the space of functions where we only take in account the derivative of greater order, that is, the space W˙  m,p(Rⁿ), is defined for m, p ∈ Z, p≥1 by

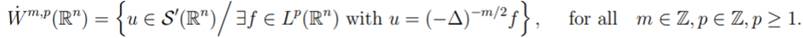
We may represent this space by

The norm in this space is defined by

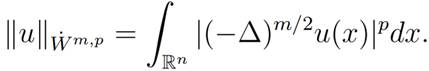
Using the inner product and norm defined above, we can show some properties involving the spaces H^s(Rⁿ). These properties have fundamental importance to show existence and uniqueness of solution for both linear and semilinear case.

Lemma 1.1: Let u ∈ H^s(Rⁿ). If 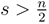 then exist a constant C > 0 such that

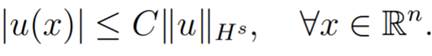
That is, when 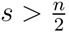 we have H^s(Rⁿ) continuously imbedding in L^∞(Rⁿ).

Lemma 1.2: (H^s(Rⁿ) is an algebra, s > n/2) Let u, w ∈ H^s(Rⁿ). If   then exist a constant C > 0 such that

This Lemma is proved in the article of Kato-Ponce and Wang-Chen.

Lemma 1.3: Let u ∈ H^s(Rⁿ). If and p ≥ 1 integer then there exist a constant C > 0 such that

Proof: For p = 1 the lemma is trivial. For p > 1 integer applying Lemma 1.2 p -1 times we get the result.

Lemma 1.4: Let u ∈ H^s(Rⁿ). If  and p > 1 integer then exist a constant C > 0 such that

Proof: definition of norm L¹(Rⁿ) we have

Using Hölder’s inequality with 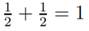 we have

The proof follows from the fact that p > 1 is integer and H^s(Rⁿ) is an algebra for

Lemma 1.5: Let u, w ∈ H^s(Rⁿ),  and p > 1 integer. Then there exist a constant C > 0 such that

Proof: Define h(λ) = λ^p then h^I(λ) = p λ^p−1. By the Mean Value Theorem we have

where

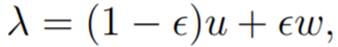
for some 0 < ∈ < 1.

Therefore, using Lemma 1.1 and the fact that p is integer, we have

 

1.1.1 Abstract Linear Problem: Existence of Solution

Let X be a Banach space and B a linear operator on X. Considering the abstract Cauchy problem

(2)

the following result holds.

Theorem 1.2: If B is the infinitesimal generator of a C₀-semigroup on X then, for each U₀ ∈ D(B) the problem (2) admits a unique strong solution

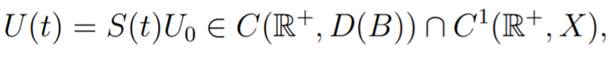
where S(t) is the semigroup generated by the operator B.

If U₀ ∈ X then we say that U(t) = S(t)U₀ ∈ C(R⁺, X) is a weak solution for (2).

Theorem 1.3: If B is the infinitesimal generator of a C₀-semigroup contractions on a Banach space X and J is a linear and bounded operator on X, then B+J is a infinitesimal generator of C₀-semigroup on X.

 

1.1.2 Abstract Semilinear Problem: Existence of Solution

Let X be a Banach space and B a linear operator on X. Consider the abstract Cauchy problem

(3)

where U₀ ∈ X, t > 0 and F is a nonlinear operator.

Definition 1.3: An operator F: D(B) → D(B) is continuous Lipschitz on bounded sets of D(B) ⊂ X if given a constant M > 0 there exist a constant L_M > 0 such that

for all U and W in D(B) such that

The next result is well known.

Theorem 1.4: Let F: D(B) → D(B) a continuous Lipschitz operator on bounded sets of D(B) ⊂ X. Then, for each U₀ ∈ D(B), there exist a unique strong solution U = U (t) of the Cauchy Problem (3) defined in a maximal interval [0, T_m) such that only one of the following conditions is true

The solution U = U(t) of Cauchy Problem (3) belongs to the following class

 

1.1.3 Tecnical Lemmas

In this section we present some lemmas that we use to prove the existence and uniqueness of solution as well as some lemmas used toget decay rates in time of the solution. Some of those lemmas have already been proved in HORBACH, J. L., IKEHATA, R. e CHARÃO, R. C.

Lemma 1.6: Let c and r be positive numbers and a ∈ R. Then, there exists a constant C > 0 such that

Lemma 1.7:  Let k > -n, ϑ > 0 and C > 0. Then there existe a constant K > 0 depending on n such that

Lemma 1.8: Let k > -n, ϑ > 0 and C > 0. Then there exist a constant K > 0 depending on n such that

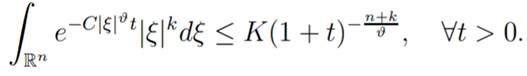
Lemma 1.9: Let n ≥ 1, a > 1 and p > 1 integer. Then, there exist a constant C = C(a, p) > 0 such that

Proof: To estimate the above integral, we separate it into two integrals, that is, an integral over the interval  and the other over .

First, we observe that, if 0 ≤ τ ≤ 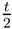 t we have 1+t ≤ 1+2t−t ≤ 2+2t−2τ ≤ 2(1+t−τ ) and this implies (1 + t − τ )^−a ≤ 2^a(1 + t)^−a, for a > 1. Then, for ap > 1, we get

Finally, we define

to get the proof of lemma for all t > 0.

 

 

2 Existence and uniqueness: linear problem

In this section using the the semigroup theory we show the existence and uniqueness of solution to the following Cauchy problem associated with an equation of Boussines/plate type with a structural rotational inertia (to the case of plates) and a fractional dissipation in Rⁿ with n ≥ 1.

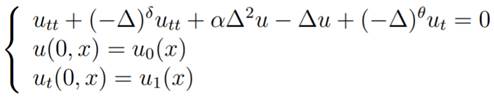
(4)

where u = u(t, x), (t, x) ∈ (0, ) Rⁿ, α > 0 is a constant. The exponents of the Laplacian operators δ and θ are such that 0 ≤ δ ≤ 2 and 0 ≤ θ ≤ .

Formally, the inner product in L²(Rⁿ) between the differential equation in (4) with u_t is given by

(5)

where the total energy E(t)) of system (4) is given by

(6)

Then, isnatural to define the energy space as

(7)

Note that in case δ > 2 we have H²(Rⁿ) ⊂ H^δ(Rⁿ) and this is unnatural because in this case u_t would be more regular than u. Another relationship we need to take care is the relationship between δ and θ because in the energy identity appears (−∆)^θ/2u_t and in the case δ ≤ θ we have H^θ(Rⁿ) ⊂ H^δ(Rⁿ). Also it is necessary to consider the relationship that comes from Luz-Ikehata-Charão (see [4]) where the condition of θ ≤ 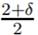 appears. To show the existence and uniqueness of solution we need consider two case between δ and θ and we rewrite the Problem (4) in a problem of first order on X as follows

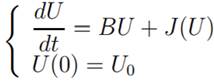
where U = (u, u_t), U (0) = (u₀, u₁) and the operators B and J depends on the cases θ < δ and θ ≥ δ.

Before we show the existence and uniqueness we need the definition of two important operators, the operators A₂ and A_θ. These operators are essential for the definition of the operator B. For the case 0 ≤ θ < δ we use the operator A₂ to define B, while in the case 0 ≤ δ ≤ θ we use the two operators, A₂ and A_θ to define the operator B.

 

2.1 The operator A_j

To define the operator A_j we need to consider j ≥ δ. We define the domain of A_j as the subspace of H^j(Rⁿ) given by2

Following the definition of D(A_j) the operator A_j, it shall be defined as

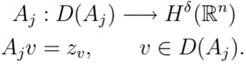
(8)

Formally we have that the operator A_j is given by

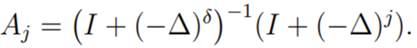
Lemma 2.1: For all v ∈ H^j(Rⁿ) exist at most one y = y_v ∈ H^δ (Rⁿ) such that

(9)

Proof: If y₁, y₂ ∈ H^δ(Rⁿ) satisfy the relation (9) and because  (Rⁿ) is dense in H^j(Rⁿ) we have

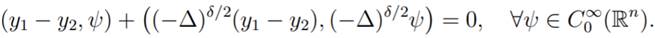
(10)

Consider   y := y₁ − y₂ , by the density of   (Rⁿ)  in  H^δ(Rⁿ), there exist {ψ_ν}_ν∈N ∈ 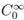 (Rⁿ) such that

therefore,

or yet

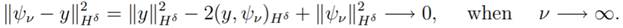
(11)

Due to

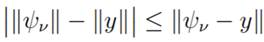
we conclude that

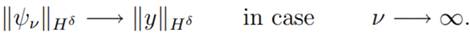
(12)

Using (11) and (12) we conclude that

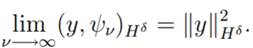
From (10) and the definition of inner product in H^δ(Rⁿ) we have

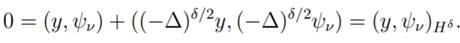
Thus, from (11) and (12) we have

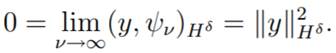
Therefore, we conclude thar y₁ = y_2.

Remark 2.1: Due to v ≡ 0 ∈ D(A_j) and Lemma 2.1 it follows that A_j is well defined.

Lemma 2.2: For j ≥ δ ≥ 0 it holds that D(A_j) H^2j−δ(Rⁿ) and there exist a constant C > 0 such that

Proof: Let v ∈ D(A_j) for definition of D(A_j), there exist y = y_v ∈ H^δ(Rⁿ) such that

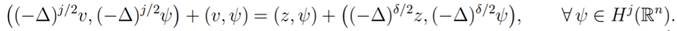
(13)

We now define the functional F₁ : H^δ(Rⁿ) −→ R by

It is easy to see that F₁ is well define and linear. Moreover, using Plancherel theorem 1.1 and the norm define in H^δ(Rⁿ) we proof that F₁ is a bounded operator. In fact

Using the density of S(Rⁿ) in H^j(Rⁿ) , the varational problem (13) takes the following form

Thus we conclude that (−∆)^jv + v = F₁ in SI(Rⁿ). Applying the Fourier Transform, where z = A_jv, we conclude

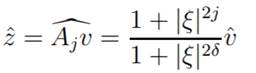
(14)

Calculating the L²(Rⁿ) norm for each term in the identity (14) we obtain

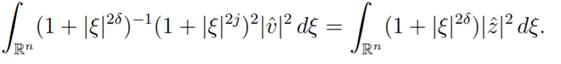
From the fact that (1 + |ξ|2δ )⁻¹(1 + |ξ|2j )² is equivalent to 1 + |ξ|2(2j−δ), we conclude that

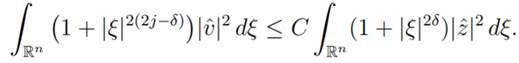
(15)

Following (15) we have that

for all v ∈ D(A_j).

Note that the condition of δ ≤ j is required, since H^2j−δ(Rⁿ) must be contained in H^j(Rⁿ).

Lemma 2.3: Let 0 ≤ δ ≤ j then H^2j−δ(Rⁿ) ⊆ D(A_j), that is, Let v ∈ H^2j−δ(Rⁿ) then there exist y ∈ H^δ(Rⁿ) such that

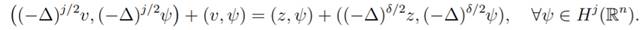
(16)

Proof: Let v ∈ H^2j−δ (Rⁿ) and G₁ : H^δ(Rⁿ) −→ R given by

Thus G₁ is well define and linear. Similarly to the proof that F₁ is continuous we may prove that G₁ is continuous (|G₁| ≤ 2\v\_H2j−δ ).

Let a₁ : H^δ(Rⁿ) × H^δ(Rⁿ) −→ R, such that a₁(ϕ, ψ) = (ϕ, ψ) + ((−∆)^δ/2ϕ, (−∆)^δ/2ψ) for all ψ, ϕ ∈ H^δ (Rⁿ).

We have that a₁(·, ·) is well defined and bilinear. Moreover a₁(·, ·) is continuous and coercive for all ϕ, ψ ∈ H^δ(Rⁿ), because

and

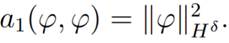
Therefore, the variational problem can be rewrite as

(17)

From the Lax-Milgram Lemma the problem (17) admits unique solution y = y_v ∈ H^δ(Rⁿ).

In particular (17) is valid for each ψ ∈ (Rⁿ), there exists only one y ∈ H^δ(Rⁿ) such that

Using the density of D(Rⁿ) in H^j(Rⁿ), by definition it follows that v ∈ D(A_j).

Remark 2.2: The Lemmas 2.2 and 2.3 they says D(A_j) = H^2j−δ (Rⁿ). When 0 ≤ δ ≤ θ we have δ ≤ θ ≤ 2θ − δ then H^2θ−δ (Rⁿ) ⊂ H^θ(Rⁿ) ⊂ H^δ(Rⁿ). When j = 2 we consider A₂ given by

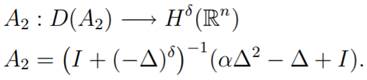
The assumption 0 ≤ δ ≤ 2 implies that δ ≤ 2 ≤ 4−δ then H^4−δ(Rⁿ) ⊂ H²(Rⁿ) ⊂ H^δ(Rⁿ).

Then, similar to the case j ≥ δ, we can see that D(A₂) = H^4−δ(Rⁿ).

 

2.2 Case 0 ≤ θ < δ and 0 ≤ δ ≤ 2

We rewrite the system (4) in matrix form, with U = (u, v) ∈ X, U₀ = (u₀, u₁) ∈ X,

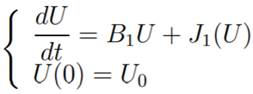
(18)

where the operator B₁ : H^4−δ (Rⁿ) × H²(Rⁿ) → X and J₁ : X → X are given by

Lemma 2.4: The operator B₁ is infinitesimal generator of contraction semigroup of class C₀ in X.

Proof: We proof that B₁ satisfies the hypotheses of Lumer-Phillips Theorem from semi-groups theory.

Let (u, v) ∈ D(B₁) = H^4−δ (Rⁿ) × H²(Rⁿ).

To proof that B₁ is dissipative we calculate the inner product

because,

According to the definition A₂. Here Img(vˆ, u¯ˆ) represents the imaginary part of vˆu¯ˆ and i = √−1. Taking the real part of B₁(u, v), (u, v) H2×Hδ we get that B₁ is dissipative.

Now we show that Im(I − B₁) = H²(Rⁿ) × H^δ(Rⁿ). It easy to prove that Im(I − B₁) ⊂ H²(Rⁿ) × H^δ (Rⁿ). We need to see that H²(Rⁿ) × H^δ(Rⁿ) ⊂ Im(I − B₁). Let (f, g) ∈ H²(Rⁿ) × H^δ(Rⁿ), then we prove that there exist (u, v) ∈ D(B₁) such that (I − B₁)(u, v) = (f, g). Equivalently, by the definition of B₁, we need to prove that there exist (u, v) ∈ D(B₁) such that (u − v, v + A₂u) = (f, g).

Thus, it is sufficient to show that there is (u, v) ∈ D(B₁) that satisfies

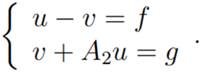
Substituting the first equality v = u − f in the second one, we have

By using the Lax-Milgran lemma we can prove that there exist u ∈ H²(Rⁿ) satisfying the identity above. In particular we can obtain A₂u + u = g + f in D^I(Rⁿ) where u ∈ H²(Rⁿ), g ∈ H^δ (Rⁿ) and f ∈ H²(Rⁿ). Then applying the Fourier transform we can rewrite the identity above as follows

Calculating the L²-norm on each side of the above identity we have

Therefore A₂u ∈ H^δ(Rⁿ). Using the definition of A₂ and Lemma 2.2 we conclude u ∈ H^4−δ(Rⁿ). Now, due to v = u − f ∈ H²(Rⁿ) it follows that v + A₂u = g is true.  We conclude that B₁ is maximal. But H^4−δ(Rⁿ) × H²(Rⁿ) is dense in the energy space X. Then by by Lumer-Phillips theorem, we obtain that B₁ is infinitesimal generator of a contraction semigroup of class C₀ in X.

Lemma 2.5: The operator J₁ : X → X is a bounded linear operator.

Proof: The fact that J₁ is linear is obvious. The prove that J₁ is bounded on X follows from the estimate

which holds because

when 0 ≤ θ < δ.

The fact that B₁ is infinitesimal generator of a contraction semigroup of class C₀ in X and J₁ is a bounded linear operator on X we conclude by theorem 1.3 that B₁ + J₁ is infinitesimal generator of a semigroup of class C₀. Let S₁ : [0, ∞) → L(X) be the semigroup of class C₀ in X generated by B₁ + J₁ then U (t) = S₁(t)U₀ is the solution of the Cauchy Problem (18).

For initial data U₀ = (u₀, u₁) ∈ X then the first component u = u(t) of U (t) = (u, u_t) is the unique weak solution of the system (4) in the class.

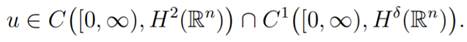
If the initial data U₀ = (u₀, u₁) ∈ D(B₁) = H^4−δ(Rⁿ) H²(Rⁿ) then u = u(t) is the unique strong solution of the system (4) and satisfies

 

2.3 Case 0 ≤ δ ≤ θ and 0 ≤ θ ≤ 2

We first observe the conditions on fractional powers, 0 ≤ δ ≤ θ and 0 ≤ θ ≤ 2, implies 0 ≤ δ ≤ 2 and because that H²(Rⁿ) ⊂ H^δ(Rⁿ). So, for the case in consideration. we can also consider again the energy space as X = H²(Rⁿ) × H^δ(Rⁿ).

Similarly to the previous section, we can consider operators B₂ and J₂. For v = u_t we have

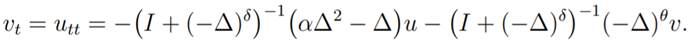
Now, considering the operators A₂ and A_θ, we can rewrite the Cauchy Problem (4) in matrix form as follows

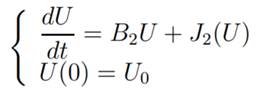
where U = U(t) = (u, v), U₀ = (u₀, u₁), and the operators B₂: H^4−δ(Rⁿ) × H²(Rⁿ) → X and J₂: X → X are given by

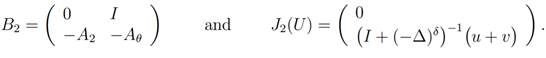
Similarly to the previous subsection, we may prove that B₂ is infinitesimal generator of a contraction semigroup of class C₀ in X and J₂ is linear and bounded on X. Then, by Theorem 1.3 we conclude B₂ + J₂ is infinitesimal generator of a semigroup of class C₀. Let S₂: [0, ∞) → L(X) the semigroup generated by B₂ + J₂. Then U(t) = S₂(t)U₀ is the unique solution of the Cauchy Problem (18) for the case on δ and θ in this subsection.

Then, for initial data U₀ = (u₀, u₁) ∈ X the first component u(t) of U(t) = S₂(t)U₀ ∈ C [0, ∞), X is the unique weak solution of the linear problem (4) and satisfies

If the initial data U₀ = (u₀, u₁) ∈ D(B₂) = H^4−δ(Rⁿ) H²(Rⁿ) then u(t) is the unique strong solution of (4) in the class

 

 

3 Decay rates: linear problem

The following theorems are proved in Charão-Horbach-Ikehata. These results show almost optimal decay rates to the norm of energy and L²-norm of the solution to the linear Cauchy problem (4).

Theorem 3.1:  Let 0 ≤ θ < δ. Then, the following decay rates are valid for the energy norm of the solution u(t, x) of (4).

Theorem 3.2: Let 0 ≤ θ < δ. Then, the following decay rates are valid for the L²-norm of solution u(t, x) of Problem (4).

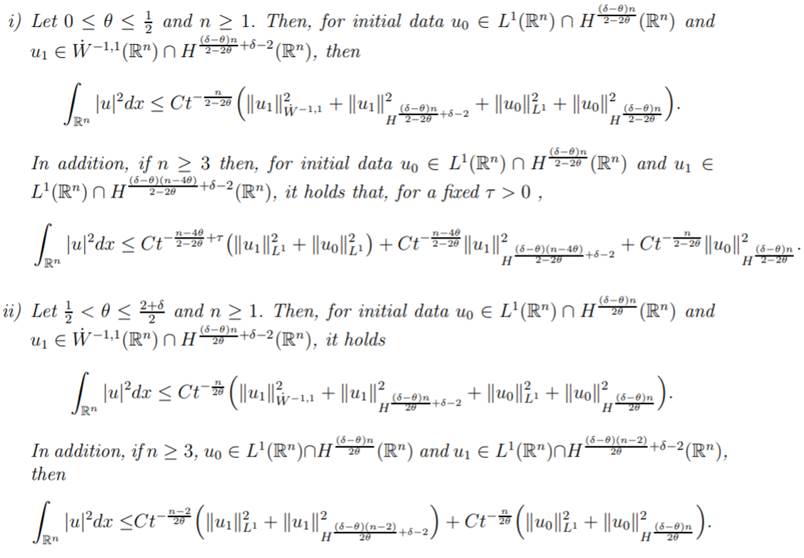
Theorem 3.3:  Let 0 ≤ δ ≤ θ and u₀ ∈ H²(Rⁿ) ∩ L¹(Rⁿ) and u₁ ∈ H^δ(Rⁿ) ∩ L¹(Rⁿ). Then, the following decay rates are valid for the energy norm of the solution u(t, x) of (4).

Theorem 3.4: Let 0 ≤ δ ≤ θ. Then the following decay rates are valid for the L²-norm of the solution u(t, x) of Problem (4).

 

 

4 Existence and uniqueness: semilinear problem

In this section we consider the Cauchy problem associated to a semilinear equation in Rⁿ of Boussineq/plate type with fractional damping given by

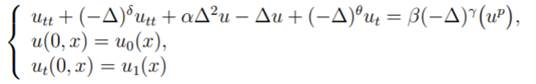
(19)

where u = u(t, x), (t, x) ∈ (0, ∞) × Rⁿ, α > 0, β /= 0 and p > 1 integer. The fractional powers of the Laplacian operator are considered as follows 0 ≤ δ ≤ 2, 0 ≤ θ ≤  and  ≤ γ ≤ .

In case δ = 2, γ = 1, p = 2 and θ = 1 we have a sixth order Boussinesq equation under the effects of a hydrodynamic dissipation (see WAANG, S. e XUE, H., 2008; DARIPA, P. e HUA, W., 2012). If θ = 0, δ = 1, γ = 1/2, β = 0 and n = 2 we have a semilinear plate equation under the effects of a frictional dissipation (see CHARÃO, R. C., DA LUZ, C. R. e IKEHATA, R, 2013; DA LUZ, C. R. e CHARAO, R. C, 2009; and SUGITANI, Y. e KAWASHIMA, S, 2013).

Similar to the linear case, to study the existence of solutions we need to consider two cases.

We reduce the order of the Cauchy Problem (19) and rewrite it in the following matrix form

where U = (u, u_t), U₀ = (u₀, u₁) and the operator B is define in the Section 3 according to the both cases above mentioned. So, in both cases B is the infinitesimal generator of a contraction semigroup of C₀-class in X. The operator F is the operator that contains the non-linear term.

 

4.1 Local Existence

To prove the local existence, since B generate a semigroup, we need only to show that the operator F is well defined as an operator F : D(B) → D(B) and it is Lipschitz continuous on bounded sets of D(B) . After prove this property of F we can take U₀ ∈ D(B) and using Theorem 1.4 one can conclude that there exist a unique solution U = U(t) in a maximal interval [0, T_m) such that one and only one of the following conditions is true.

In addition, we have U ∈ C¹ [0, T_m), X ∩ C [0, T_m), D(B).

 

4.1.1 Case 0 ≤ θ < δ and 0 ≤ δ ≤ 2

To show the local existence for this case, we should consider the fractional power γ in the interval 0 ≤ γ ≤ 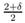 . As in the linear case we consider the usual energy space X and we rewrite the system (19) in the matrix form

where U = (u, v) ∈ X, U₀ = (u₀, u₁) ∈ X and the operators B₁ : H^4−δ(Rⁿ)×H²(Rⁿ) → X and F₁ : D(B₁) → D(B₁) are given by

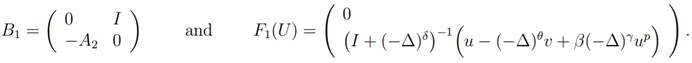
Lemma 4.1: The operator F₁ : D(B₁) → D(B₁) is well define for 0 ≤ γ ≤  and n < 8 − 2δ.

Proof: We consider U = (u, v) ∈ D(B₁) and we show that F₁(u, v) ∈ D(B₁). By definition of F₁ and norm in H² we have

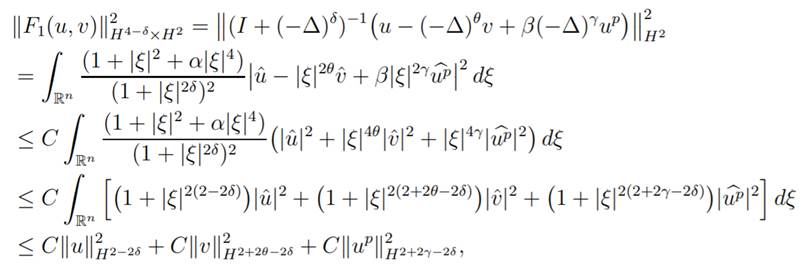
due to the assumptions 2 − 2δ ≤ 4 − δ, 2 + 2θ − 2δ < 2 and 2 + 2γ − 2δ ≤ 4 − δ.

Thus, from the definition of norm in H^s(Rⁿ) and the natural embedding of H^s(Rⁿ) in H^r(Rⁿ) for s ≥ r, we get the following estimate

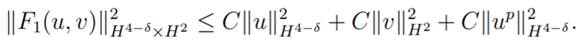
Now using Lemma 1.3 with s = 4 − δ, we obtain for n < 8 − 2δ

Lemma 4.2: Let 1 ≤ n < 8 − 2δ, 0 ≤ θ < δ, 0 ≤ δ ≤ 2, 0 ≤ γ ≤  and p > 1 integer. let U = (u, v) and W = (w, z) such that U, W ∈ D(B₁) = H^4−δ (Rⁿ) × H²(Rⁿ). Then

Proof: For U = (u, v) and W = (w, z) in H^4−δ(Rⁿ) × H²(Rⁿ) we have

because 2θ − δ < 2 and 2γ − δ ≤ 4 − δ.

Now, using Lemma 1.5 with s = 4 − δ, for n < 8 − 2δ we have

The estimate (see lemma 2.2) ||u||_H4−δ ≤ C||A₂u||_Hδ for all u ∈ D(A₂) and the defini- tion of operator B₁ imply that

Lemma 4.3: Let 1 ≤ n < 8 − 2δ, 0 ≤ θ < δ, 0 ≤ δ ≤ 2, 0 ≤ γ ≤  and p > 1 integer. Let U = (u, v) and W = (w, z) such that U, W ∈ D(B₁) = H^4−δ(Rⁿ) × H²(Rⁿ). Then there exist a constant C > 0 such that

Proof: For U = (u, v) and W = (w, z) in H^4−δ(Rⁿ) × H²(Rⁿ) we have

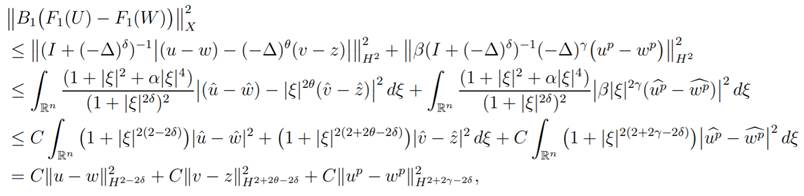
since we have assumed 2 − 2δ ≤ 4 − δ, 2 + 2θ − 2δ < 2 and 2 + 2γ − 2δ ≤ 4 − δ.

The above estimate combined with lemma 1.5 imply for n < 8 − 2δ the estimate of lemma.

Finally, combining the Lemmas 4.2 and 4.3 we conclude that

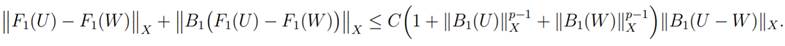
Therefore, given a constant M > 0 and considering U, W ∈ H^4−δ (Rⁿ) H²(Rⁿ) such that

we have, for L_M = 1 + 2M^p−1, the following estimate

Thus, we conclude that F₁ is Lipschitz continuous on bounded sets of D(B₁). Then, the fact that B₁ is infinitesimal generator of a contraction semigroup of C₀-class in X, using the Theorem 1.4 we have the following theorem of local existence and uniqueness.

Theorem 4.1: Let 0 ≤ θ < δ, 0 ≤ δ ≤ 2, 0 ≤ γ ≤ 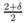, p > 1 integer and 0 < n < 8 − 2δ. Then, for initial data (u₀, u₁) ∈ H^4−δ(Rⁿ) × H²(Rⁿ) there exist unique solution to the semilinear Cauchy Problem (19) defined in a maximal interval [0, T_m) in the class

satisfying one and only one of the following conditions

 

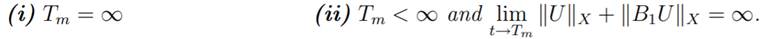
4.1.2 Case 0 ≤ δ ≤ θ and 0 ≤ θ ≤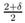

We write the system (19) in the standard matrix form as in previous section

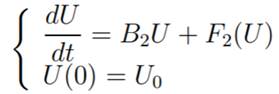
where the operators B₂ : H^4−δ(Rⁿ) × H²(Rⁿ) → X and F₂ : D(B₂) → D(B₂) are given by

Similar to the previous section we prove, also in this case, that F₂ is well defined and is Lipschitz continuous on bounded sets of D(B₂).  In section 2 we proved that B₂ is infinitesimal generator ofa contraction semigroup of C₀-class in X. Then, using the Theorem 1.4 we obtain the local of existence and uniqueness as follows.

Theorem 4.2: Let 0 ≤ δ ≤ θ, 0 ≤ θ ≤ , 0 ≤ γ ≤ , p > 1 integer and 0 < n < 8 − 2δ. Then, for initial data (u₀, u₁) ∈ H^4−δ(Rⁿ) × H²(Rⁿ) there exist a unique solution to the semilinear Cauchy Problem (19) in a maximal interval [0, T_m) in the class

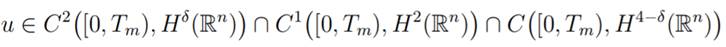
such that one and only one of following conditions is true

 

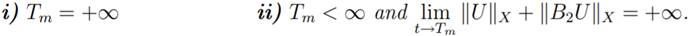
4.2 Global Existence

In this section we show that the maximal interval  of existence in the two previous cases  is [0, ∞). To do that, we assume T_m < ∞ and we claim that ||U ||_X + ||BU ||_X < +∞. In such case we get T_m = ∞ and the global existence follows.

Taking the Fourier Transform in spatial variable x on the Cauchy problem (19) we get the equivalent Cauchy problem in Fourier space

(20)

Using the Duhamel principle the solution of the Cauchy Problem 20 can be write as

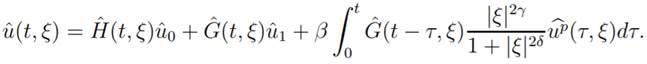
(21)

Then, the derivative in time is given by

(22)

where the fundamental solutions to the linear problem are

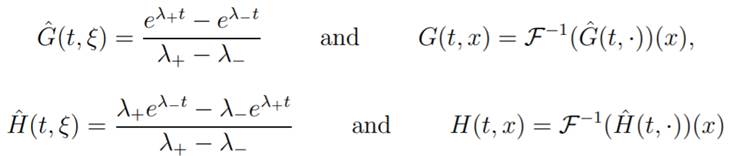
and the associated characteristics roots are

In the HORBACH, J. L., IKEHATA, R. e CHARÃO, R. C., 2016 is calculated in Lemma 3.6 the following estimate to solutions of the linear problem.

(23)

We use the estimate (23) to prove the next lemma.

Lemma 4.4:  Let Gˆ(t, ξ)  and  Hˆ(t, ξ)  fundamental  solutions  of  linear  problem  associated to Problem (20). Then we have the following estimates:

Proof: To show items (i) and (ii) we consider the solution of the homogeneous problem (20) with uˆ₀ = 0. Then, we have uˆ(t, ξ) = Gˆ(t, ξ)uˆ₁ and uˆ_t(t, ξ) = Gˆt (t, ξ)uˆ₁.

Substituting these expressions on the left hand side of the estimate (23) the result for (i) and (ii) follows. The proof of item (iii) and (iv) is similar.

Now, to prove the claim that || U||_X +   ||BU||_X < + ∞ we need consider again the two cases on δ and θ.

 

4.2.1 Case 0 ≤ θ < δ and 0 ≤ δ ≤ 2

We need in this case to show that the norm ||U(t) ||_X + ||B₁U(t) ||_X is bounded for all t ∈ [0, T_m) by assuming that T_m < +∞.

By definition of B (u, u_t) = (u_t, −A₂u), where A₂ = (I + (−∆)^δ) −1(α∆²−∆ +I), we have

We note that

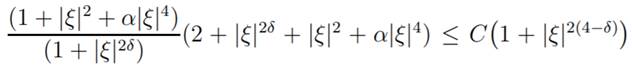
and

(2 + |ξ|2δ + |ξ|2 + α|ξ|4 ) ≤ C 1 + |ξ|4

for all ξ ∈ Rn, Then, we obtain

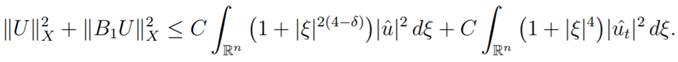
Substituting uˆ and uˆ_t, given by (21) and (22) respectively, in the above inequality we have

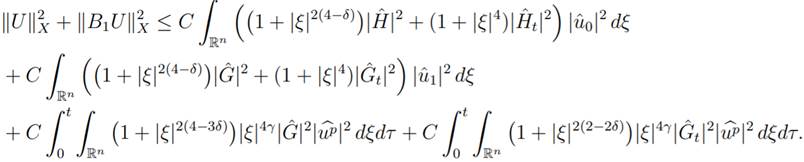
Now, using the estimates in Lemma 4.4 and the fact that  ≤ 1 we obtain

(24)

We observe that in the second integral at the right hand side of (24) uˆ₁ appears a singularity given by |ξ|−2. So, this term is a little delicate to deal with in the zone of low frequency, that is, ξ near zero. To do that we assume additional regularity on the initial data u₁. In the third integral we have the same singularity but it is controlled by the term |ξ|4y from the nonlinearity because γ ≥ 1/2.

Note that, for |ξ| ≥ 1 we have

and for 0 < |ξ| ≤ 1 we have

Using these estimates, we estimate the integral where appears the initial data  uˆ₁ em (24)  working at  the zones of low and high frequency. The integral on high frequency is estimate by  and the integral on the low frequency  is  estimate  by  the  norm  of  u₁  in  W˙  −1,1(Rⁿ).  The other integrals at the right hand side of (24) can be estimate in standard way. Therefore, we conclude that

Using the Lemma 1.3 with 0 < n < 8 − 2δ we have for p > 1 integer

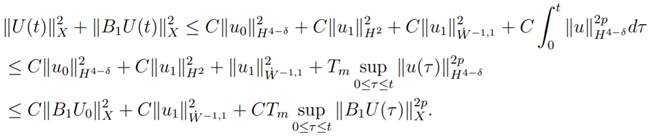
(25)

for all t ∈ [0, T_m) with the maximum time of existence T_m is assumed to be finite.

Now, we define the function

From the previous inequality we get that M₁(t) satisfies

(26)

In order to show that the solution obtained to the Cauchy Problem (19) is global, that is T_m = +∞, we need the next elementary lemma of calculus.

Lemma 4.5: Let p > 1 and F (M) = aI₀ + bT M^p − M a continuous positive function on M ≥ 0, with a, b, I₀, T positive constants. Then, there exist a unique M₀ > 0 absolute minimum point of F (M) in [0, ∞). In addition, there exist ε > 0 such that F (M₀) < 0 if 0 < I₀ ≤ ε.

We note that the function M₁(t) is not negative and satisfy F (M₁(t)) ≥ 0 for all t ∈ [0, T_m) due to inequality (26) with F(M) the function given in Lemma 4.5 with

Therefore, if 0 < I₀ ≤ ε, ε > 0 given by Lemma 4.5, due to the continuity of the function M₁(t), there are only two possibilities:

However, we note that

Then, assuming another condition on the initial data  that  M₁(0)  <  M₀ (M₀ the  global  minimum point  in  Lemma 4.5)  it follows that M₁(t) ≤ M₀ for all t ∈ [0, T_m). Them the condition that holds is (i). Therefore, if T_m is finite, we have proved that

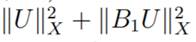
is bounded for all t ∈ [0, T_m). This contradicts the condition of Theorem 4.1. Then, we must have T_m = ∞ and the solution is global for the case in consideration. The result is

Theorem 4.3: Let 0 ≤ θ < δ, 0 ≤ δ ≤ 2, 1 ≤ γ ≤ 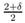, p > 1 integer and 1 ≤ n < 8 − 2δ. Consider  the  initial  data  u₀ ∈ H^4−δ(Rⁿ) and  u₁ ∈ H²(Rⁿ) ∩ W˙  −1,1(Rⁿ) satisfying  0  < I₀ ≤ ε and M₁(0) < M₀ with ε, I₀, M₀, M₁(0) given above and in Lemma 4.5.

Then, there exist a unique global solution u = u(t, x) to the Cauchy Problem (19) such that

 

4.2.2 Case 0 ≤ δ ≤ θ and 0 ≤ θ ≤

To this case, we need to find a upper bound for the norm ||U ||_X +||B₂U ||_X for all t ∈ [0, T_m), with U = (u, u_t) where u is the solution of (19) given by Theorem 4.2. Analogously to the previous section we may obtain such estimate. This fact proves that the solution is global and the following result holds.

Theorem 4.4:  Let  0 ≤ δ  ≤ θ, 0 ≤ θ ≤ ,  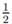≤ γ ≤ , p > 1 integer and 1 ≤ n < 8 − 2δ. Consider the initial data u₀ ∈ H^4−δ(Rⁿ) and u₁ ∈ H²(Rⁿ) ∩ W˙  −1,1(Rⁿ) satisfying 0 < I₀ ≤ ε and M₂(0) < M₀ with ε, I₀, M₀, M₂(0) given in a similar way as in previous case. Then, for this case on δ and θ, there exist unique global solution u = u(t, x) to the Cauchy Problem (19) such that

 

 

5 Decay rates: semilinear problema

From Theorems 4.3 and 4.4 the semilinear Problem (19) has a unique global solution in the class

for all 0 ≤ δ ≤ 2, 0 ≤ θ ≤ 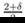,  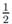≤ γ ≤ , p > 1 integer and 1 ≤ n < 8 − 2δ. Consider the initial data u₀ ∈ H^4−δ(Rⁿ) and u₁ ∈ H²(Rⁿ) ∩ W˙  −1,1(Rⁿ) small enough.

In this section we show decay rates to the energy and L²(Rⁿ) norm of the solution to the semilinear problem (19) by using estimates similar to the estimates in previous sections.

We note that is sufficient to get estimates for the norm || (u, u_t) || _H4−δ ×H2 to obtain decay rates to the energy norm and L²(Rⁿ)-norm. In fact, it holds that

(27)

Let us now find an estimate for || (u, u_t) || _H4−δ×H2. In section 4.2 we have expressions for the solution uˆ and its derivative uˆ_t (see (21) and (22)). Then, using such expressions and the definition of norm H^4−δ × H² we obtain

Now, by considering the estimates in Lemma 4.4 we arrive at the estimate

(28)

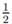We note here that the terms that appear in the above inequality can be estimated for, 0 ≤ δ ≤ 2, 0 ≤ θ ≤  and  ≤ γ ≤ , for all ε ∈ Rⁿ, as follows

As in (24) we can observe that in the estimate (ii) above appears the singularity  |ξ|−2 for ξ  near zero which is controlled by the term |ξ|^4γ since we have assumed γ ≥ 1/2  On the second integral at the right hand side of the last estimate, as in (24), we do not have the term |ξ|4γ  because that we assume the additional hypotheses u₁ ∈ W˙  −1,1(Rⁿ) . The problem with such singularity is at the zones of low frequency. The integral on high frequency can be estimate in standard way.

In fact, to estimate the coefficient of |uˆ₁|2, we see that for |ξ| ≥1

because |ξ|2(1 + α|ξ|2) ≥ (1 + α|ξ|4 ).

tghuis, using the above estimates, we may conclude that || (u, u_t) || _H4−δ×H2 is bounded by the four integrals as shown below

At this point, we define the following integrals, dependent on t, which appear in the above estimate

The function ρ_θ define in section 3 depends on θ, then we separated the problem into four cases:

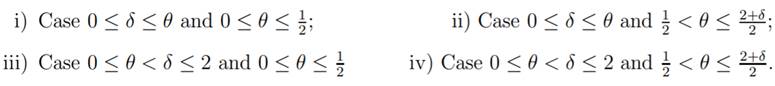
In the next subsections we show decay estimates to the energy and for the L²-norm of the solution in cases (i) and (ii). These estimates refer to the case 0 ≤ δ ≤ θ where we do not need to impose more regularity on the initial data compared to the decay rates was already obtained to the liner problem. The cases (iii) and (iv) can be estimated in the same way but assuming regularity on the initial data.

 

5.1 Case 0 ≤ δ ≤ θ and 0 ≤ θ ≤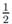

In this subsection we find decay rates to the L²-norm and to the energy for the semilinear problem.

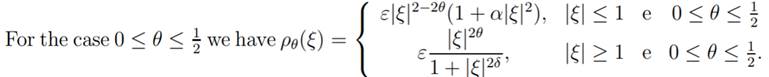
Since ρ_θ = ρ_θ (ξ) also depends on ξ, we estimate in the low and high frequency in the following way

Lemma 5.1: Let p > 1 integer and 1 ≤ n < 8 − 2δ. Let θ, δ and γ  such that 0 ≤ δ ≤  θ, 0  ≤  θ  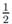 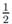≤ ,  ≤  γ  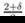 ≤ .  Then, for all initial data u₀ ∈ H^4−δ(Rⁿ) ∩ L¹(Rⁿ) and u₁ ∈ H²(Rⁿ) ∩ L¹(Rⁿ) ∩ W˙  −1,1(Rⁿ) we have

Proof: We start estimating L₁ defined above. First we separated the integral into two integrals, at the low frequency (|ξ| ≤ 1) and another at the high frequency (|ξ| ≥ 1). Then we get

We use the Lemma 1.8 to estimate the integral at the low frequency and the definition of norm in H^s(Rⁿ) to estimate the integral at the high frequency. Thus we obtain

In the same way we can easily estimate L₂ to get

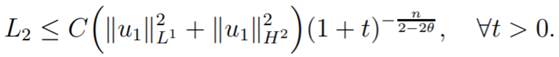
The estimate for L3 follows from the definition of the Sobolev space  W˙  −1,1(Rⁿ) and from Lemma 1.8. Then we have for t > 0

To get an estimate to N₁ we again estimate the associated integral into low frequency and high frequency as follows

On the low frequency zone we use the Lemmas 1.8 and 1.1 and on high frequency we use the Lemma 1.3 with n < 8 − 2δ. Then, since 2 + 2γ − 2δ ≤ 4 − δ  and the condition that γ ≤ 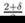 we arrive at the estimate

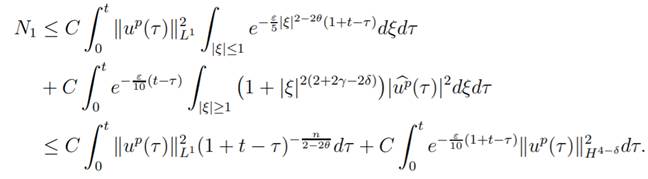
Now, using the Lemmas 1.3 and 1.4 with n < 8 − 2δ and p > 1 integer, we have estimates to L¹-norm and H^4−δ-norm of u^p. Thus the estimate for N₁ is obtained as

Therefore, combining the above estimates, we conclude for p > 1 integer and n < 8−2δ

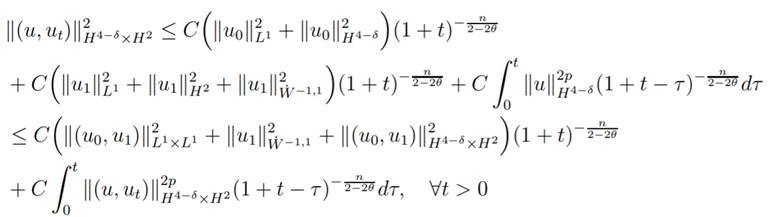
and the lemma is proved.

Finally we multiply the inequality in previous lemma by  in order to get the following inequality which holds for t > 0.

Now, for t ≥ 0 we define the function

(29)

From the above inequality we have

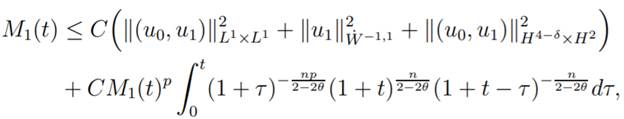
for all t > 0. By Lemma 1.9 we have

when , that is, 2 −2θ < n with C(n, p, θ) a positive constant.

Therefore, we have arrived at the following main inequality with holds for t > 0.

(30)

Finally, to find the desired decay rates to the Cauchy Problem (19) we need an elementary lemma of calculus, analogous to Lemma 4.5.

Lemma 5.2: Let p > 1 and F (M) = aI₀ + bM ^p − M, a continuous and positive function for M ≥ 0, and a, b, I₀ positive constants. Then, there exist only one M₀ > 0 absolute minimum point of F(M) in [0, ∞). In addition, there exist ε > 0 such that if 0 < I₀ ≤ ε then F(M₀) < 0.

Combining (30), the above lemma and work as in subsection 4.2 we can prove the following theorem.

 

Theorem 5.1: Let 0 ≤ δ ≤ θ, 0 ≤ θ ≤ 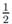, 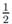 ≤  γ   ≤ , p > 1 integer and 2 − 2θ < n < 8 − 2δ. Consider  the initial data u₀ ∈ H^4−δ(Rⁿ) ∩ L¹(Rⁿ) and u₁ ∈ H²(Rⁿ) ∩ L¹(Rⁿ) ∩ W˙  −1,1(Rⁿ) satisfying 0 < I₀ ε and M₁(0) < M₀ with ε, I₀, M₀, M₁(0) given by Lemma 5.2. Then the following estimate for the energy norm plus the L² standard of the solution is true

We note here that the rate found above is the same rate found for the energy norm of Linear Problem 4 as we see in Theorem 3.3 item (i).

 

5.2 Case 0 ≤ δ ≤ θ and 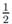 < θ   ≤

As in the previous section we prove decay rates to the energy and L²-norm for this case. The result is the following.

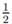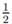Theorem 5.2: Let 0 ≤ δ ≤ θ,  < θ ≤,  ≤ y ≤, p > 1 integer and 2θ < n <8 − 2δ. Consider  the initial data u₀ ∈ H^4−δ(Rⁿ) ∩ L¹(Rⁿ) and u₁ ∈ H²(Rⁿ) ∩ L¹(Rⁿ) ∩ W˙  −1,1(Rⁿ) satisfying  0  <  I₀ ε  and  M₂(0)  <  M₀ with  ε,  I₀,  M₀,  M₂(0)  define  above. Then the following estimate for the energy norm plus the L² standard of the solution is true

Remark 5.1: We observe that we can remove the hypotheses γ ≥ 1/2 in Theorems 4.3, 5.1, 5.2 and assume the condition γ ≥ max {0, ½ − n/4} by performing a simple estimate. In fact such condition was imposed when was estimated the integral corresponding to the semilinear term in (24) and in (28) on the zone of low frequency. Indeed, we can estimate the integral with a singularity in ξ = 0 that appears in (24).

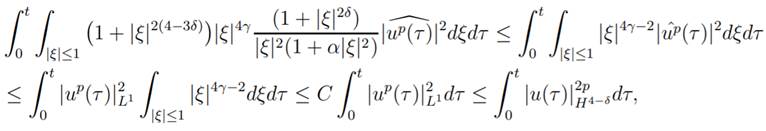
due to Lemma 1.4 for 4 − δ > n/2 and the assumption γ > 1/2 − n/4 with γ > 0.

 

 

References

CHRISTOV, C. I., MAUGIN, G. A. e VELARDE, M. G. Well-posed Boussinesq paradigm with purely spatial higher-order derivatives.  Physical Review  E,  v.  54, n. 4, p. 3621-3638, 1996.

CHARÃo, R.  C., DA LUZ, C.  R.  e IKEHATA, R.  New decay rates for a problem of plate dynamics with fractional damping. Journal of Hyperbolic Differential Equations, v. 10, n. 3, p. 563-575, 2013.

DA LUZ, C. R. e CHARA˜O, R. C. Asymptotic properties for a semilinear plate equa- tion in unbounded domains. Journal of Hyperbolic Differential Equations, v. 6, n. 2, p. 269-294, 2009.

DA LUZ, C. R., IKEHATA, R. e CHARA˜O, R. C. Asymptotic behavior for abstract evolution differential equations of second order. Journal of Differential Equations, v. 259, n. 10, p. 5017-5039, 2015.

DARIPA, P. e HUA, W. A numerical study of an ill-posed Boussinesq equation aris- ing in water waves and nonlinear lattices: Filtering and regularization techniques. Applied Mathematics and Computation, v. 101, n. 2-3, p. 159-207, 1999.

ESFAHANI, A., FARAH, L. G. e WANG, H. Global existence and blow-up for the gen- eralized sixth-order Boussinesq equation. Nonlinear Analysis:  Theory, Methods and Applications, v. 75, n. 11, p. 4325-4338, 2012.

HORBACH, J. L., IKEHATA, R. e CHARA˜O, R. C. Optimal Decay Rates and Asymp- totic Profile for the Plate Equation with Structural Damping. Journal of Mathe- matical Analysis and Applications, v. 440, n. 2, p. 529-560, 2016.

IKEHATA, R. e NATSUME, M. Energy decay estimates for wave equations with a fractional damping. Differential and Integral Equations, v. 25, n. 9-10, p. 939-956, 2012.