Universidade Federal de
Santa Maria
Ci.
e Nat., Santa Maria v.42, Special Edition: 40 anos, e2, 2020
DOI:10.5902/2179460X39940

40 years - anniversary
The
long-term inverse Nakagami distribution: Properties, inference and application
A
distribuição Nakagami inversa de longo termo: propriedades, inferência e
aplicação
Francisco
Louzada Neto
Pedro Luiz Ramos
Paulo
Henrique Ferreira da Silva
I
Institute
of Mathematical and Computer Sciences, University of São Paulo, São Carlos,
Brazil. E-mail: louzada@icmc.usp.br.
II
Institute
of Mathematical and Computer Sciences, University of São Paulo, São Carlos,
Brazil. E-mail: pedrolramos@usp.br.
III Institute of
Mathematical and Computer Sciences, University of São Paulo, São Carlos, Brazil.
E-mail: paulohenri@ufba.br.
ABSTRACT
In this paper, a new
long-term survival distribution, the so-called long-term inverse Nakagami
distribution, is presented. The proposed distribution allows us to fit data
with unimodal hazard function, where a part of the population is not
susceptible to the event of interest, the so-called long-term survival. This
distribution can be used, for instance, in clinical studies where a portion of
the population can be cured during a treatment. Some mathematical properties of
the new distribution are derived. The inferential procedures for the parameters
are discussed under the maximum likelihood estimators. A numerical simulation
study is carried out to verify the performance of these estimators. Finally, an
application to real data on patients’ lifetime after acute myocardial
infarction illustrates the usefulness of the proposed distribution.
Keywords: Acute myocardial
infarction; Cure fraction; Inverse Nakagami distribution; Long-term survival
distribution; Maximum likelihood estimation.
RESUMO
Neste artigo, uma nova distribuição
de longa duração é introduzida, denominada distribuição de longa duração
inversa Nakagami. A distribuição proposta nos permite ajustar dados com a
função de risco unimodal, em que uma parte da população não é suscetível ao
evento de interesse. Este modelo pode ser usado, por exemplo, em estudos
clínicos em que uma parte da população pode ser curada durante um tratamento.
Algumas propriedades matemáticas do novo modelo são apresentados. Os
procedimentos inferenciais para os parâmetros são discutidos sob os estimadores
de máxima verossimilhança. Um estudo de simulação numérica é realizado para
verificar o desempenho desses estimadores. Finalmente, uma aplicação a dados
reais sobre o tempo de vida de pacientes após infarto agudo do miocárdio
ilustra a utilidade do modelo proposto.
Palavras-chave: Infarto agudo do miocárdio; Fração
de cura; Distribuição inversa Nakagami; Distribuição de longa duração;
Estimação por máxima verossimilhança.
1 INTRODUCTION
Deriving lifetime distributions has been of great interest
among researchers for decades. Lifetime
distributions can be motivated
by either mathematical or lifetime
issues (i.e., physical
principles) interest (Ristic´ e Nadarajah, 2014).
However, regardless of their motivation, new lifetime distributions are often required
in order to provide reasonable fittings for a broad spectrum
of real-world datasets.
Indeed, real-world datasets may possess peculiar characteristics that can not
be appropriately addressed by the existing
distributions.
In this sense, Louzada et al. (2018) recently
proposed the inverse Nakagami (INK) distribution. Let T be
a random variable with an INK distribution, then its probability density
function (PDF) is given by
|
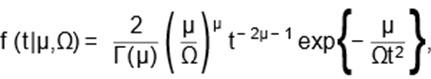
|
(1)
|
for all t > 0, where Γ(µ) =  e−ttµ−1dt is the gamma function, µ > 0
and Ω
> 0 are the shape and scale parameters,
respectively. The INK distribution contains some important
sub-models, such as the inverse
Rayleigh (µ = 1), inverse
half-normal (µ
= 0.5), inverse chi (Ω
= 1, µ = ν/2, and ν = 1,2, . . .) and inverse Hoyt (0
< µ < 1) distributions. The authors showed
that the INK distribution has unimodal hazard rate function, regardless of the
parameter values.
e−ttµ−1dt is the gamma function, µ > 0
and Ω
> 0 are the shape and scale parameters,
respectively. The INK distribution contains some important
sub-models, such as the inverse
Rayleigh (µ = 1), inverse
half-normal (µ
= 0.5), inverse chi (Ω
= 1, µ = ν/2, and ν = 1,2, . . .) and inverse Hoyt (0
< µ < 1) distributions. The authors showed
that the INK distribution has unimodal hazard rate function, regardless of the
parameter values.
The use of unimodal hazard rate function
is very realistic
when describing the lifetime of a patient
susceptible to disease.
For instance, Chowell e Nishiura (2014) argued that Ebola virus has a mean incubation period of 12.7 days, with an infectious mean period of 6.5 days.
Additionally, the mean lifetime from illness onset to death is ten days. In this case, the risk of the patient dying from this particular virus
first increases over time, but after a period decreases, i.e., it has a unimodal
hazard rate. Although
Ebola is highly fatal (its fatality
ratio is between
61% and 89% in Zaire; see Chowell e Nishiura (2014)
and the references therein), the
population may not experience the death related to the disease. This
characteristic is known as cure fraction.
The long-term survival
models, also known as cure rate models,
have been widely
used in the literature. Berkson
e Gage (1952) proposed the existence of two subpopulations, susceptible and non-susceptible to the event
of interest, which
leads to the standard
mixture long-term survival model. Chen et al. (1999) further proposed the
promotion time long-term survival model, which is based on the Poisson
distribution. Rodrigues et al. (2009) unified the different long-term survival
models by using a general structure for the different latent
activation mechanisms, which
leads to the long-term survival models. Many distributions have been
considered as baseline distributions of the models
cited above. For instance, Cordeiro
et al. (2016) considered the negative binomial distribution for the latent variable distribution, where the baseline
survival distribution is the Birnbaum-Saunders. Gallardo et al. (2017) proposed the Pareto IV power
series long-term survival model. Ramos et al. (2017) considered the standard
mixture long-term survival distribution with the Fréchet
distribution, and named it as the long-term Fréchet distribution. Furthermore, the so-called “defective” models have also been used by many
authors to describe data with long-term survivals (Balka et al., 2011; Santos
et al., 2017; Rocha et al., 2017).
In this paper, we propose the long-term inverse
Nakagami (LINK) distribution, which is based on the standard mixture long-term survival
distribution, where the baseline distribution is the INK distribution. The INK distribution is useful to describe
patients’ lifetime data, where the susceptible group has a unimodal hazard
rate. Several mathematical properties of the proposed distribution are derived and discussed. The parameter estimation is considered under
the maximum likelihood estimators (MLEs).
The LINK distribution is then used to describe the lifetime of patients after
acute myocardial infarction in Rio de Janeiro city,
Brazil. This dataset was firstly presented in Melo et al. (2004) and
indicated an elevated long-term survivals fraction among the patients, which
can be accurately estimated by our new distribution.
The remainder of the paper
is organized as follows. Section
2 reviews the INK distribution. Section 3 presents
the new LINK distribution. Section 4 discusses
parameter estimation using the maximum likelihood method. Section 5 introduces
a simulation study aiming to verify the performance of the MLEs. Section 6 illustrates
the relevance of our proposed methodology in a real lifetime data. Finally,
Section 7 summarizes the study.
2 INK Distribution
The mean and variance of the INK distribution (1)
are given, respectively, by
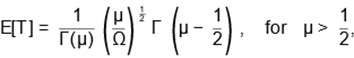
and

Moreover, its survival and hazard rate
functions are given, respectively, by
|
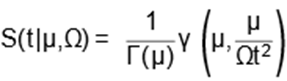
|
(2)
|
and
|
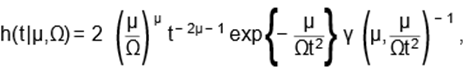
|
(3)
|
where γ(y,x) = 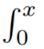 wy−1e−wdw is
the lower incomplete gamma function. As commented before in Section 1, the
hazard rate function (3) is unimodal for all µ > 0 and Ω > 0.
wy−1e−wdw is
the lower incomplete gamma function. As commented before in Section 1, the
hazard rate function (3) is unimodal for all µ > 0 and Ω > 0.
The results above, as well as other
mathematical properties of the INK distribution, including its r-th
moment, r-th central moment, mean residual life function and Shannon’s
entropy, are presented in Louzada et al. (2018).
3 Long-term survival Model
An important characteristic to be taken into
account when modeling lifetime data is the existence of long-term survivors,
i.e., a portion of the population which may not be susceptible to the event
of interest (see, e.g., Maller e Zhou, 1995; Perdoná e Louzada-Neto, 2011).
In this case, we suppose
that the population is split into two groups:
those patients that are not susceptible to the event of interest with probability π, and those who are susceptible (in risk) to the event with probability (1 –π). The long-term survival
function is then given by
|
Spop(t) = π + (1 − π)S0(t),
|
(4)
|
where π 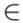 (0,1) and S0(t) denotes the baseline survival function for the susceptible group in
the population.
(0,1) and S0(t) denotes the baseline survival function for the susceptible group in
the population.
The obtained (unconditional) survival function (4), which represents the survival function
for the entire population, is improper
and limt→∞ Spop(t) = π. From (4), one can easily
derive the probability sub-density function (PSDF) given by
|
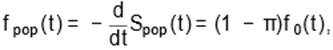
|
(5)
|
where f0(t) is the baseline PDF for the susceptible individuals. Hence, from (4)
and (5), we obtain the hazard rate function
|

|
(6)
|
In this paper, we assume that f0(t) follows
an INK distribution. Then, it follows from (1) and (5) that the PSDF of the
LINK distribution is give
|
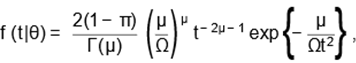
|
(7)
|
where θ = (µ, Ω ,π) denotes the parameter vector.
The r-th moment of T is
By considering (2) and (4), we obtain the
improper survival function of the LINK distribution
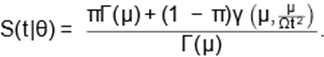
Figure 1 shows the shape of the PSDF and the
improper survival function of the LINK distribution, for some parameter values.
Figure 1 - Left panel: PSDF of the LINK
distribution. Right panel: improper survival function of the LINK distribution.
Finally, from (1), (2) and (6), we have the hazard rate function of the LINK
distribution
Finally, from (1), (2) and (6), we have the
hazard rate function of the LINK distribution:
|
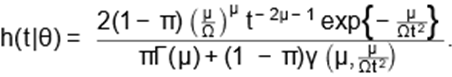
|
(8)
|
Note that
|

|
(9)
|
and
|
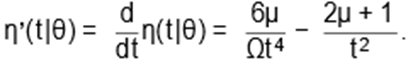
|
(10)
|
Glaser (1980) proved that, for a non-negative
continuous random variable with twice-differentiable PDF (or PSDF, in our case), if η(t|θ) has a unimodal
shape, then h(t|θ)
has also a unimodal shape. For all µ > 0 and Ω > 0, we have that (9) is
unimodal shaped, with a global maximum at t∗ =  (which
is obtained by equaling (10) to zero). Therefore, (8) is
also unimodal shaped. shaped. Figure
2 shows
the shape of the hazard function of the LINK
distribution.
(which
is obtained by equaling (10) to zero). Therefore, (8) is
also unimodal shaped. shaped. Figure
2 shows
the shape of the hazard function of the LINK
distribution.
Figure 2 - Hazard
shape of the LINK distribution for different values of µ, Ω and π
4
Inference
Suppose that the lifetime of the i-th
patient may not be observed and is subject to right-censoring. Moreover,
consider that the random censoring times Ci’s are independent of the true lifetimes Ti’s, and the distribution of Ci’s does not depend on the parameters governing the distribution of Ti’s. Then, for a sample of size n, the dataset
is D = {(ti,δi) : i = 1, . . . ,n}
, where ti = min {Ti,Ci} and δi = I(Ti≤Ci), with I(.) denoting
an indicator function. This random censoring scheme has as special cases the
types I and II censoring schemes. The likelihood function is given by

Let T1, . . . ,Tn be a random sample of size n
from the LINK distribution (7). Then, the likelihood function, considering data
with random censoring, is given by
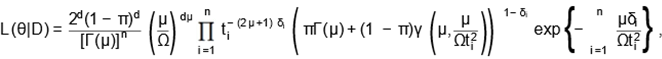
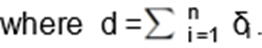
The log-likelihood function is given by
|
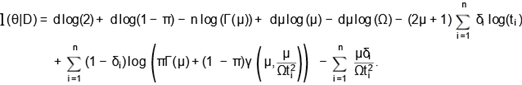
|
(11)
|
The maximum likelihood method is the most
widely used approach for estimating parameters, since it provides estimators (MLEs) that have several desirable properties, such as asymptotic efficiency, consistency and invariance.
The MLEs θˆ of θ are obtained from the solution
of ∂l(θ|D)/∂µ = 0, ∂l(θ|D)/∂Ω = 0 and ∂f(θ|D)/∂π = 0. Hence, the likelihood
equations are given as follows:

and

Where  is the digamma function;
is the digamma function; 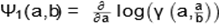 and
and  can be calculated
numerically. Numerical methods need to be used to find the solution (maximum
likelihood estimates) of these nonlinear equations.
can be calculated
numerically. Numerical methods need to be used to find the solution (maximum
likelihood estimates) of these nonlinear equations.
Under mild regularity conditions, the MLEs are
consistent, efficient and asymptotically normally distributed with a joint
trivariate normal distribution given by
θˆ ∼ N3 θ,I−1(θ) for n → ∞,
where I(θ) is the 3 × 3 Fisher
information matrix for θ, and Iij(θ) is the (i,j)-th element of I(θ) given by
Note, however,
that it is not possible to compute the Fisher information matrix I(θ) due to the presence of censored observations (censoring is random and
non-informative). Thus, one alternative approach is to use the observed
information matrix H(θ) evaluated at θˆ, i.e. H(θˆ), whose terms
are given by
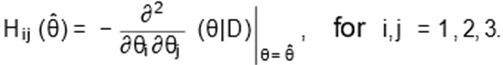
Large-sample (approximate) confidence intervals
at level 100(1 − ξ)%, for each
parameter θi, i = 1, 2, 3, can be calculated as

where zξ/2 denotes the (ξ/2)-th quantile of a standard normal distribution.
As discussed earlier, we have considered maximization
procedures to find the solution of the MLEs. The use of good initial values play an important
role to achieve convergence of the estimates
with less computational cost. The starting
values for Ω and π
can be obtained by
|
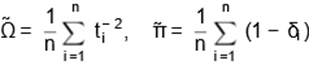
|
(12)
|
and µ can
be estimated by
|

|
(13)
|
The initial values
for µ and
Ω are derived
following the closed-form estimators for complete
data proposed by Louzada et al.
(2018). The initial value for π is
obtained as the proportion of censored data (in this case, it is expected
that the long-term survivals fraction will be smaller than the proportion of censoring). Observe
that we expect to get biased estimates
from the equations
above. On the other hand, these biased estimates allow us to initiate
the Newton-Raphson algorithm closer to the maximum likelihood estimates than
using random values.
Figure 3
- MREs, MSEs and CPs related to the ML estimates of µ = 0.5, Ω = 2 and π = 0.4, for N = 100,000 simulated samples and
different values of n
5 Simulation Study
In this section, a Monte Carlo simulation study
is provided to investigate the performance of the maximum likelihood (ML)
method. This procedure is conducted by computing the mean relative estimate
(MRE) and the mean square error (MSE), which are given by
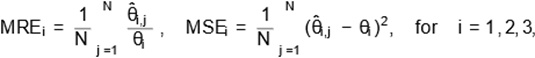
where N = 100,000 is the number of ML estimates (or Monte Carlo
samples). Additionally, we compute the coverage probabilities (CPs) of the 95% asymptotic
confidence intervals. Under the proposed metrics, we expect that the MLEs
return MREs close to one with small
MSEs. Moreover, for a 95% confidence level, the proportion of intervals that cover the true parameter value should be close
to 0.95.
The parameter values used to perform the
simulations are: µ=0.5, Ω =2 and π=0.4 (Figure 3); µ
= 1.5, Ω =
6 and π =
0.5 (Figure 4); µ=2, Ω=4 and π=0.6 (Figure
5), where n={50,60, . . . ,400}
. Note that we have
considered the scenarios where the long-term survivals fraction is 0.4,
0.5, and 0.6, respectively. The assumed censoring scheme is random. Hence we
may observe different proportions of censoring for each dataset. In these
scenarios, the observed mean proportion of censorship is roughly 0.454, 0.638,
and 0.724, respectively. It is important to point out that other parameter
values were also considered and similar results were obtained. The R software (R
Core Team, 2014) was used to obtain
the results, where the maxLik package (Henningsen e Toomet, 2011) was considered to find the
maximization of the log-likelihood function (11). Moreover, this procedure is
well-behaved, and we have not faced
numerical problems, such as failure of convergence or end on multiple maxima.
Figure 4
- MREs, MSEs and CPs related to the ML estimates of µ =
1.5, Ω = 6 and π = 0.5, for N = 100,000 simulated samples and different values of n
Figures 3 - 5 present the MREs, MSEs and CPs of
the ML estimates of µ, Ω and π,
for different values of n. The
horizontal line in these plots corresponds to MRE, MSE, and CP equal to one, zero and 0.95, respectively. As one can see from these figures,
the MLEs of µ, Ω and π
are asymptotically unbiased, since the MREs tend to
one and the MSEs decrease to zero as n increases. Moreover, with CPs tending to 0.95 when n becomes large, good coverage properties may be deliberated for the MLEs. Thus, in practical applications, the ML
estimation method will be relevant, as shown in the next section.
Figure 5 - MREs,
MSEs and CPs related to the ML estimates of µ = 2, Ω = 4 and
π = 0.6, for N = 100,000 simulated
samples and different values of n
6 Acute Myocardial Infarction Data
In this section, we consider a real dataset
related to the lifetime (in days) of 3,077 patients after acute myocardial
infarction (AMI). They were admitted to the Brazilian
National Health System
(Sistema Único de Saúde, or SUS in Portuguese), in Rio de Janeiro
city, Brazil, during the year 2000.
This dataset was firstly analyzed by Melo et al. (2004) and can be fully
accessed at http://sobrevida.fiocruz.br/infarto.html.
In order to compare different models (including
our proposed LINK distribution), we consider three long-term lifetime
distributions: the long-term Fréchet (LF) distribution (Ramos et al., 2017), the
well-known long-term Weibull distribution
(LW) and the long-term weighted
Lindley (LWL) distribution (Louzada
e Ramos, 2017). The LF distribution has PSDF given by
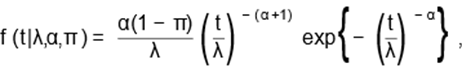
for t > 0, where λ > 0, α > 0 and π ∈ (0,1) are,
respectively, the scale, shape and mixing parameters. This
distributionparameter estimation under the ML approach is performed using the
results presented in Ramos et al. (2017). Additionally, the LW distribution has
PSDF given by
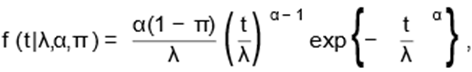
for t,λ,α > 0 and π ∈ (0,1). Finally, the PSDF of the LWL distribution is given by
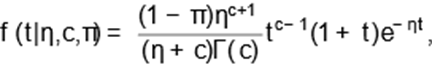
for t,η,c > 0 and π ∈ (0,1). The
inference for this distribution parameters is conducted using the same steps as
discussed by the main authors.
The results obtained using the LINK
distribution are compared to the corresponding ones achieved with the use of
the long-term lifetime models described above. In order to select which
distribution to use, we consider different discrimination criteria, such as the AIC (Akaike
Information Criterion) and AICc (Corrected Akaike Information Criterion), which are calculated by  and
and , where k is the number of parameters
to be estimated. For a set of
candidate models that fitted the data at hand, the preferred distribution is the one that provides
the minimum AIC and AICc values.
, where k is the number of parameters
to be estimated. For a set of
candidate models that fitted the data at hand, the preferred distribution is the one that provides
the minimum AIC and AICc values.
Figure 6 shows the fitted
survival functions superimposed to the empirical survival function
(Kaplan-Meier estimate). From this figure, we can see that the LINK
distribution gives a better fit to the patient’s lifetime data.
Figure 6 - Long-term
(improper) survival function adjusted by different distributions and the
Kaplan-Meier (KM) estimator, considering the dataset related to patients’
lifetime after AMI in Rio de Janeiro, Brazil (year 2000)
Table 1 presents the negative log-likelihood (-log L), AIC and AICc values for different long-term
lifetime models. It can be observed from this table that the LINK distribution provides a better
fit to these data since
the adjusted distribution has the lowest values in all criteria.
Table 1 - The -log
L, AIC and AICc values for the fitted distributions, considering the dataset
related to patients’ lifetime after AMI in Rio de Janeiro, Brazil (the year
2000)
|
|
LF
|
LW
|
LWL
|
LINK
|
|
-log L
|
2873.4
|
2933.4
|
2985.5
|
2857.4
|
|
AIC
|
5752.8
|
5872.7
|
5976.9
|
5720.9
|
|
AICc
|
5752.8
|
5872.7
|
5976.9
|
5720.9
|
The parameter estimates of the LINK
distribution were obtained using the same procedure as described in Section 4. The
initial values determined from (12) and (13) were Ω˜ = 0.03879, π˜ = 0.84433 and µ˜ = 0.14296, and only 10 iterations were necessary to achieve the ML estimates using the Newton-Raphson maximization algorithm. Table 2 exhibits the ML estimates, the standard errors (SE) and the 95% confidence intervals (95%
CI) for µ, Ω and π.
Table 2 - ML
estimates, SE and 95%
CI for the parameters of the LINK distribution,
considering the proposed dataset
|
Parameter
|
Estimate
|
SE
|
95% CI
|
|
µ
|
0.1450
|
0.00061
|
(0.0966; 0.1935)
|
|
Ω
|
0.1680
|
0.00051
|
(0.1238; 0.2123)
|
|
π
|
0.7709
|
0.00049
|
(0.7275; 0.8144)
|
The hazard function
for the proposed
dataset is available in Figure 7. The curve shown in this figure
describes the instantaneous death rate for the patients
that had AMI. In this case, we can observe that the patients have a higher chance of death in the first
days. On the other hand, as time goes by, the
hazard rate decreases until they are not susceptible to death by AMI.
Figure 7 - Hazard
curve of the LINK distribution fitted to the proposed dataset
Therefore, through our proposed methodology, the dataset related
to the lifetime of patients
after AMI in Rio de Janeiro, Brazil, can be well-described by the LINK distribution.
7 Discussion
In this paper, we have derived a new
distribution named long-term inverse Nakagami distribution, which can
accommodate long-term survivals fraction in survival analysis. The proposed
distribution has unimodal hazard function, which is realistic for describing
the lifetime of patients that may not experience the event of interest. The
mathematical properties of the new distribution were discussed. The maximum likelihood estimators of the parameters and their asymptotic properties were presented. The simulation study showed
that the maximum likelihood method provides efficient estimators for unknown
parameters and returns good coverage probabilities as the sample size increases.
The long-term inverse
Nakagami distribution was used to describe the lifetime of patients that had acute myocardial infarction. In this case, we concluded that the long-term
survivals fraction of the patients
was 0.7709, i.e., the patients
that had not died from that condition.
Many extensions of the present work can be
considered. For instance, covariates can be included in the long-term survival
term to improve the prediction, e.g., using the logistic link function given by
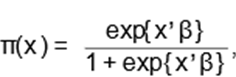
where β = (β0,β1, . . . ,βp) is the vector of parameters related
to the vector of covariates x = (1,x1, . . . ,xp) . Another approach that can be
considered is the use of Bayesian methods to improve the estimates for small
samples. Future work will investigate such proposals.
Disclosure statement
No potential conflict of interest was reported
by the authors.
Acknowledgements
Francisco Louzada and Pedro L. Ramos acknowledge support from the São Paulo
State Research Foundation (FAPESP Processes 2013/07375-0 and 2017/25971-0, respectively).
References
Balka,
J., Desmond, A. F., McNicholas, P. D. (2011). Bayesian and likelihood
inference for cure rates based on defective inverse Gaussian regression models.
Journal of Applied Statistics, 38(1), 127–144.
Berkson,
J., Gage, R. P. (1952). Survival curve for cancer patients following treatment.
Journal of the American Statistical Association, 47(259),
501–515.
Chen,
M. H., Ibrahim, J. G., Sinha, D. (1999). A new Bayesian model for survival data
with a surviving fraction. Journal of the American Statistical Association,
94(447), 909–919.
Chowell,
G., Nishiura, H. (2014). Transmission dynamics and control of Ebola virus
disease (EVD): a review. BMC
Medicine, 12(1),
196.
Cordeiro, G. M., Cancho,
V. G., Ortega, E. M. M., Barriga, G. D. C. (2016). A model with long-term survivors: negative binomial
Birnbaum-Saunders. Communications in Statistics-Theory and Methods, 45(5), 1370–1387.
Gallardo,
D. I., Gómez, Y. M., Arnold, B. C., Gómez, H. W. (2017). The Pareto IV power
series cure rate model with applications.
SORT-Statistics and
Operations Research Transactions, 41(2), 297–318.
Glaser, R. E. (1980).
Bathtub and related
failure rate characterizations. Journal of the American Statistical Association, 75(371),
667–672.
Henningsen, A., Toomet,
O. (2011). maxLik:
A package for maximum likelihood estimation in R. Computational Statistics, 26(3), 443–458.
Louzada,
F., Ramos, P. L. (2017). A
new long-term survival distribution. Biostatistics and Biometrics Open
Access Journal, 1(4), 1–6.
Louzada,
F., Ramos, P. L., Nascimento, D. (2018). The inverse Nakagami-m distribution: A
novel approach in reliability. IEEE Transactions on Reliability, 67(3),
1030–1042.
Maller,
R. A., Zhou, S. (1995). Testing for the presence of immune or cured individuals
in censored survival data. Biometrics, 51(4), 1197–1205.
Melo, E. C. P., Travassos, C. M. R., Carvalho, M. S. (2004).
Infarto agudo do miocárdio no Município do Rio de Janeiro: qualidade dos dados, sobrevida e
distribuição espacial. Tese de Doutorado.
Perdoná, G. C., Louzada-Neto, F. (2011).
A general hazard
model for lifetime
data in the presence of cure rate. Journal of Applied
Statistics,
38(7), 1395–1405.
R
Core Team (2014). R: A Language
and Environment for Statistical Computing. (Version
3.3.1). R Foundation for Statistical Computing, Vienna, Austria.
Ramos,
P. L., Nascimento, D., Louzada, F. (2017). The long term Fréchet distribution:
Estimation, properties and its application.
Biometrics &
Biostatistics International Journal, 6(3), 00,170.
Ristic´, M. M., Nadarajah, S. (2014). A new lifetime distribution. Journal of Statistical
Computation and Simulation, 84(1),
135–150.
Rocha, R., Nadarajah, S., Tomazella, V., Louzada,
F. (2017). A new class of defective models
based on the Marshall-Olkin family of distributions for cure rate
modeling. Computational
Statistics & Data Analysis,
107, 48–63.
Rodrigues, J., Cancho, V. G., de Castro,
M., Louzada-Neto, F. (2009).
On the unification of long-term survival
models. Statistics & Probability Letters, 79(6), 753–759.
Santos, M. R., Achcar,
J. A., Martinez, E. Z. (2017). Bayesian and maximum
likelihood inference for the defective Gompertz cure rate
model with covariates: an application to the cervical carcinoma study. Ciência e Natura, 39(2), 244–258.
e−ttµ−1dt is the gamma function, µ > 0
and Ω
> 0 are the shape and scale parameters,
respectively. The INK distribution contains some important
sub-models, such as the inverse
Rayleigh (µ = 1), inverse
half-normal (µ
= 0.5), inverse chi (Ω
= 1, µ = ν/2, and ν = 1,2, . . .) and inverse Hoyt (0
< µ < 1) distributions. The authors showed
that the INK distribution has unimodal hazard rate function, regardless of the
parameter values.