Universidade Federal de Santa Maria

Ci. e nat., Santa Maria, v. 42

Commemorative Edition: Statistic, e15, 2020

DOI: http://dx.doi.org/10.5902/2179460X40386

Received: 05/10/2019 Accepted: 10/10/2020

Statistics

Modelos volumétricos para o tronco da erva-mate (Ilex paraguariensis A. St.-Hil.): uma análise através das técnicas de regressão

Volumetric models for mate herb (Ilex paraguariensis A. St .- Hil.): through an analysis of techniques for regression

Gabriel Dalla Costa Berger^I

Ivanor Müller^II

Fernando de Jesus Moreira Junior^III

Angela Pelegrin Ansuj^IV

^I Universidade Federal de Santa Maria, Brasil; e-mail: gabriel@gabrielberger.com.br;

^II Universidade Federal de Santa Maria. Brasil. e-mail: ivanormuller@smail.ufsm.br;

^III Universidade Federal de Santa Maria, Brasil; e-mail: fmjunior777@yahoo.com.br;

^IV Universidade Federal de Santa Maria. Brasil. e-mail: angelaansuj@yahoo.com

RESUMO

Este trabalho teve como objetivos a modelagem volumétrica para erva-mate através da análise de regressão, selecionando o modelo que melhor se ajuste aos dados utilizados; bem como determinar o volume rigoroso ou real de cada árvore pelo método analítico. Foram avaliadas trinta (30) árvores. Em cada árvore foram medidas as variáveis biométricas altura total em metros (ht), diâmetro dos troncos a 0,60 metros acima do solo (d 0.6 metros), raio médio de copa em metros (rc), área de copa em metros quadrados (ac). Para a construção das equações para estimar o volume de madeira com casca e sem casca utilizou-se o pacote estatístico Statistical Analisys System versão 8. Foi utilizado o método Stepwise de seleção de variáveis independentes, em que se limitou ao máximo a inclusão de três variáveis nas equações selecionadas, e o R2 parcial da variável independente superior a 1% para considerá-la significativa. O teste de seleção de equações foi realizado com e sem intercepto. Os resultados apresentados pelas equações sem intercepto foram superiores às equações com intercepto, tendo sido então desprezado esses últimos. A média da altura, diâmetro, raio de copa, área de copa, volume com casca e volume sem casca foram respectivamente: 2,9650 m, 4,4696 cm, 1,1607 m, 4,1382 m2, 0,0139 m3, e 0,0108 m3. O desvio padrão para a altura, diâmetro, raio de copa, área de copa, volume com casca e volume sem casca foram respectivamente: 0,5600 m, 0,8997 cm, 0,2299 m, 1,5895 m2 , 0,0075 m3, 0,0050 m3 . O valor mínimo para a altura, diâmetro, raio de copa, área de copa, volume com casca e volume sem casca foram respectivamente: 2,0000 m, 2,9600 cm, 0,7502 m, 1,7789 m2, 0,0055m3, 0, 0,0042 m3. O valor máximo para a altura, diâmetro, raio de copa, área de copa, volume com casca e volume sem casca foram respectivamente: 4,5000 m, 6,1300 cm, 1,7600 m, 8,1433 m3, 0,0367m3, 0,0231m3. A equação selecionada para estimar o volume com casca foi a seguinte: vcc = 0,01273*ln(h). A equação selecionada para estimar o volume sem casca foi a seguinte: vsc = 0,00076*hd.

Palavras chave: Erva-mate, Análise de Regressão, Modelagem.

ABSTRACT

This work aimed at the volumetric modeling for maté tea by the regression analysis, selecting the model that best fit the data used, and determine the volume of each tight or real tree by analytical method. Were evaluated thirty (30) trees. in each tree were measured variables biometric total height in meters (ht), the diameter of the trunks 0.60 meters above the ground (d 0.6 meters), medium radius of crown in meters (rc), the crown area in square metres (ac). For the construction of the equations to estimate the volume of wood with no bark and bark used in the statistical package Analisys Statistical System version 8. Stepwise was used the method of selection of independent variables, which limited the maximum the inclusion of three variables in the equations selected, and the R2 part of the independent variable over 1% to consider it significant. The test of selection of equations was performed with and without intercept. The results presented by the equations without intercept was higher than equations with intercept, and was then despised these latest. The average height, diameter, radius of crown, the crown area, volume and volume in shell shelled were respectively: 2.9650 m, 4.4696 cm, 1,1607 m, 4,1382 m2, 0,0139 m3, and 0.,0108 m3. The standard deviation for height, diameter, radius of crown, the crown area, volume and volume in shell shelled were respectively: 0,5600 m, 0,8997 cm, 0,2299 m, 1,5895 m2, 0,0075 m3, 0,0050 m3. The minimum value for height, diameter, radius of crown, the crown area, volume and volume in shell shelled were respectively: 2,0000 m, 2,9600 cm, 0,7502 m, 1,7789 m2, 0,0055 m3 , 0,0042 m3. The maximum value for the height, diameter, radius of crown, the crown area, volume and volume in shell shelled were respectively: 4,5000 m, 6,1300 cm, 1,7600 m, 8,1433 m3, 0,0367 m3 , 0,0231 m3. The equation selected to estimate the volume with bark was: vcc = 0,01273 * ln (h). The equation selected to estimate the volume without bark was: vsc = 0,00076 * hd.

Keywords: Mate tea, Regression Analysis, Modeling.

1. INTRODUÇÃO

O cultivo da erva-mate (Ilex paraguariensis A. St.-Hil.), na Região Sul do Brasil apresenta importância socioeconômica e ambiental (ROSSE; FERNANDES, 2002), sendo uma atividade importante para a geração de emprego e renda aos produtores e às propriedades rurais situados na região de cultivo da espécie (BERGER, 2006). As suas folhas são utilizadas para a fabricação de erva-mate para chimarrão enquanto que o tronco pode ser utilizado como fonte de matéria-prima para diversos fins. No entanto, as exigências ecológicas da erva-mate quanto às condições de solo, clima, fornecimento de água e nutrientes, para o cultivo da espécie ainda são pouco conhecidas, pois grandes variações de crescimento e produção de biomassa são observadas quando se cultiva e produz erva-mate em diferentes tipos de solo (BERGER, 2006).

Segundo Berger (2006), a erva-mate, bem como outras espécies nativas, ainda é carente de estudos e pesquisas que possibilitem aumentar os benefícios de sua exploração econômica, pois os estudos dendrométricos existentes são mais relacionados com espécies de rápido crescimento, principalmente os gêneros Pinus spp e Eucalyptus spp, embora a erva-mate quando cultivada para fins econômicos também apresenta um crescimento rápido, mas, apenas suas folhas juntamente com os talos apresentam importância econômica. A erva-mate, na maioria das vezes, deixa de ser estudada devido à inexistência de informações relativas ao seu crescimento e biometria, o que dificulta o seu correto manejo.

Embora o principal objeto de comercialização seja a folha (ROSSE; FERNANDES, 2002), o tronco da erva-mate também pode ser utilizado para diferentes fins com casca e sem casca. Dessa forma, torna-se importante mensurar o volume do tronco nessas duas situações. Assim, esse trabalho teve como objetivo ajustar o melhor modelo para determinar o volume do tronco com casca e sem casca através de modelos de regressão.

2. METODOLOGIA

Este estudo foi realizado na Fazenda Tupi, município de Nova Prata, RS, localizada na região nordeste do Estado, propriedade pertencente a Paludo Agropecuária S.A., empresa do grupo VIPAL. A propriedade possui 962 ha de área total, sendo 780 ha de Floresta Ombrófila Mista em estágio médio e avançado de desenvolvimento, onde há abundância de formas de vida vegetal, conforme Leite (2002). Quanto à infra-estrutura local, a Fazenda Tupi possui vias de acesso asfaltado até 2 km da sede, serraria para uso próprio na manutenção da fazenda, energia elétrica, telefone, e equipamentos básicos, necessários ao plantio, manutenção e colheita da erva-mate.

Segundo Herrmann e Rosa (1991), a unidade de relevo que ocorre na região é do tipo Planalto das Araucárias e o local está situado na parte intermediária da serra e as declividades médias do local não ultrapassam 30%.

A altitude média do local é de 750 m, e o solo da região classificado como latossolo vermelho distrófico típico, profundo e bem drenado, são solos que têm pouco incremento de argila e são imtemperizados (STRECK, 2002).

O clima, segundo Moreno (1961), é classificado por Köeppen como Cfb, caracterizado como temperado, com temperatura do mês mais quente inferior a 22^oC e a do mês mais frio entre –3^oC e 18^oC, sendo a temperatura média anual inferior a 18,5^oC. A precipitação média anual oscila entre 1.750 e 2.468 mm, regularmente distribuída ao longo do ano.

A vegetação na região, segundo Veloso et al. (1991), é do tipo fitogeográfico: Floresta Ombrófila Mista, com o domínio de Myrtaceas e Nectandras no sub-bosque e, no extrato superior, destaca-se a araucária.

Foram escolhidas aleatoriamente 30 árvores em uma área de aproximadamente 400 hectares. As idades das árvores variavam de 10 a 12 anos de idade, com espaçamento entre as árvores de 1 m x 2,5 m. Em cada uma das 30 árvores, foram medidas as seguintes variáveis biométricas: diâmetro dos troncos a 0,60 m acima do solo (d0,6 m), altura total da erveira (h), e área de copa (ac).

O diâmetro foi obtido com auxílio de um paquímetro (precisão de 0,01 cm). Por causa das podas regulares que são submetidas as erveiras, não foi possível definir um tronco principal para cada planta, então definiu-se o d0,6 como sendo a média aritmética dos troncos à altura de 0,60 m acima do solo.

A altura de cada árvore foi determinada através de uma régua de 3 m, com precisão de 0,1 m, do solo ao ápice da árvore. O raio médio da copa (rc) em metros (m), foi obtido pela média aritmética de quatro medições à altura de 1,30 m acima do solo nos sentidos norte, sul, leste e oeste.

A área de copa (ac) das erveiras em m² foi calculada partindo do raio médio da copa (rc) e aplicada a fórmula do círculo. Após medidas essas variáveis em todas as 30 árvores, foram cortadas ao nível do solo e separadas em cinco classes de diâmetros para facilitar a coleta de dados para mensuração do volume, como mostra a Tabela 1.

Tabela 1 – Divisão da madeira em classes de diâmetro.

Classe de Diâmetro	Diâmetro (cm)
CD1	0,1 – 1,09
CD2	1,1 – 2,09
CD3	2,1 – 3,09
CD4	3,1 – 5,09
CD5	> 5,1

O volume rigoroso com casca e sem casca de cada classe foi determinado por meio da cubagem de Newton e Huber. Pelo método de cubagem por Newton, em cada fuste foi realizado a leitura do diâmetro em três pontos distintos, uma no topo, uma no centro e uma na base. De acordo com Husch et al. (1982) apud Machado e Figueiredo Filho (2003), a fórmula de Newton é a mais acurada para todas as formas de fuste.

Com estas leituras, foi possível calcular o volume do tronco com casca de cada fuste. A seguir, nas mesmas posições onde foi feito a leitura do diâmetro do tronco com casca, foram retiradas as cascas para a leitura do diâmetro do tronco sem casca onde foi calculado o volume do tronco sem casca de cada fuste da erva-mate. Em galhos inferiores a 15 cm de comprimento, foi utilizado o método de Huber. Com os volumes do tronco com e sem casca, foi possível calcular o volume de casca e a porcentagem de casca existente na erva-mate obtido pela diferença entre os volumes.

As variáveis dependentes obtidas com base nas 30 árvores cortadas foram o volume do tronco com casca e o volume do tronco sem casca. As variáveis dependentes e as variáveis independentes (d0,6 m, h, ac) utilizadas na modelagem e suas transformações estão apresentadas na Tabela 2.

Tabela 2 – Variáveis dependentes e independentes utilizadas na modelagem.

variáveis dependentes
Y1	vcc	volume com casca
Y2	vsc	volume sem casca
variáveis independentes
X1	d 0,6 m	média dos diâmetros a 60 cm do nível do solo
X2	h	altura total da erveira
X3	ac	área de copa
X4	h^2	altura total ao quadrado
X5	h^3	altura total ao cubo
X6	d^2	diâmetro ao quadrado
X7	d^3	diâmetro ao cubo
X8	hd	altura vezes diâmetro
X9	ac^2	área de copa ao quadrado
X10	ac^3	área de copa ao cubo
X11	dh^2	diâmetro vezes altura ao quadrado
X12	d^2h	diâmetro ao quadrado vezes altura
X13	dh^3	diâmetro vezes altura ao cubo
X14	hd^3	altura vezes diâmetro ao cubo
X15	d^2h^2	diâmetro ao quadrado vezes altura ao quadrado
X16	d^3h^3	diâmetro ao cubo vezes altura ao cubo
X17	ach	área de copa vezes altura
X18	acd	área de copa vezes diâmetro
X19	ach^2	área de copa vezes altura ao quadrado
X20	acd^2	área de copa vezes diâmetro ao quadrado
X21	lnd	logaritmo neperiano do diâmetro
X22	lnh	logaritmo neperiano da altura
X23	lnac	logaritmo neperiano da área de copa
X24	lnac^2	logaritmo neperiano da área de copa ao quadrado
X25	lnac^3	logaritmo neperiano da área de copa ao cubo
X26	ln^2d	logaritmo neperiano ao quadrado vezes diâmetro
X27	ln^2h	logaritmo neperiano ao quadrado vezes altura
X28	1/h	inverso da altura
X29	1/d	inverso do diâmetro
X30	1/hd	inverso da altura vezes o diâmetro
X31	1/h^2	inverso da altura ao quadrado
X32	1/d^2	inverso do diâmetro ao quadrado
X33	1/h^3	inverso da altura ao cubo
X34	1/d^3	inverso do diâmetro ao cubo
X35	1/d^2h	inverso do diâmetro ao quadrado vezes altura
X36	1/dh^2	inverso do diâmetro vezes altura ao quadrado
X37	1/d^2h^2	inverso do diâmetro ao quadrado vezes altura ao quadrado
X38	1/d^3h^3	inverso do diâmetro ao cubo vezes altura ao cubo

Foi utilizado o método Stepwise Backward de seleção de variáveis independentes, em que se limitou ao máximo a inclusão de três variáveis nas equações selecionadas. Para verificar a qualidade do ajuste dos modelos foi utilizado o coeficiente de determinação ajustado (R² aj), considerando nível de significância de 1%. Além disso, foi utilizado como critério que a uma variável independente só seria incluída no modelo se houvesse um aumento maior de 1% no valor do R² aj. O teste de seleção de equações foi realizado com e sem intercepto. Para verificar a significância dos coeficientes do modelo utilizou-se o teste t, com nível de significância de 1%. Para construção das equações para melhor representar o volume do tronco com casca e sem casca utilizou-se o pacote estatístico Statistical Analisys System - SAS - versão 8.

3. RESULTADOS

A seguir são apresentados os modelos obtidos para estimar o volume do tronco da erva-mate com casca e sem casca, respectivamente.

3.1 Modelo para estimar o volume do tronco com casca

            Durante o procedimento Stepwise Backward, verificou-se que os resultados apresentados pelas equações sem intercepto foram superiores aos resultados das equações com intercepto, assim foram analisadas somente as equações sem intercepto.

A Tabela 3 apresenta os resultados obtidos para a variável selecionada. Observa-se que apenas a variável lnh foi inserida no modelo, pois não houve outra variável que aumentasse o valor do R² ajustado em mais de 1%, consequentemente, foram excluídas. O modelo estimado para esta variável explica 75,31% das observações.

Tabela 3 – Resultados pelo método Stepwise Backward para o volume do tronco com casca.

Passo	variável inserida	R^2aj	F	p-valor
1	lnh	0,7531	92,50	<0,0001

R²aj = coeficiente de determinação ajustado; F = valor de F para a equação, p-valor = nível de significância para F.

A Tabela 4 apresenta a variável independente selecionada com o seu parâmetro estimado e respectivo o resultado do teste t. Observa-se que variável é significativa (p<0,0001) para o modelo.

Tabela 4 – Resultado da estimativa dos parâmetros para o volume com casca.

variável	parâmetro estimado	t	p-valor
lnh	0,01273	9,62	<0,0001

t = valor de t para a equação, p-valor =  nível de significância para t.

A Tabela 5 mostra os resultados obtidos para a análise da variância para o modelo ajustado. Observa-se que o modelo ajustado é significativo (p-valor < 0,0001).

Tabela 5 – Resultado da análise de variância para o modelo ajustado.

Fonte	GL	SQ	QM	F	p-valor
Modelo	1	0,0057	0,00573	92,50	<0,0001
Erro	29	0,0018	0,00006
Total	30	0,0075

GL = grau de liberdade SQ = soma dos quadrados; QM = quadrado médio; F = valor de F; p-valor = nível de significância.

Após a seleção das variáveis, chegou-se ao seguinte modelo para determinar o volume do tronco com casca:

vcc = 0,01273*lnh

em que:

vcc = volume com casca em metros cúbicos;

lnh = logaritmo neperiano da altura.

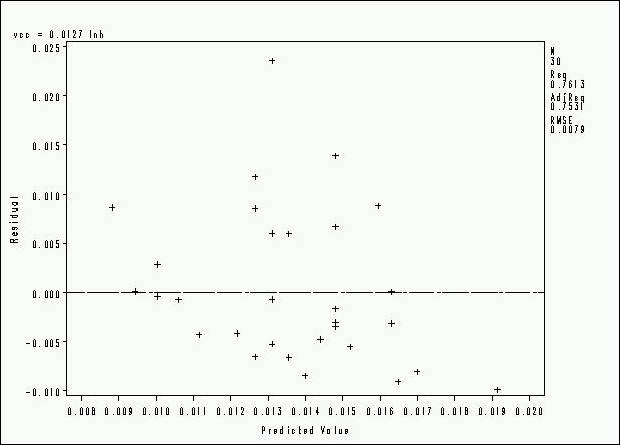
A distribuição dos resíduos do modelo ajustado para estimar o volume com casca pode ser observada na Figura 1. Pode-se observar que os resíduos do modelo ajustado são independentes e normalmente distribuídos com média zero e variância constante, o que comprova que o modelo ajustado é adequado.

Figura 1 – Distribuição dos resíduos da equação selecionada para estimar o volume com casca.

3.2 Modelo para estimar o volume do tronco sem casca

            Durante o procedimento Stepwise Backward, verificou-se que os resultados apresentados pelas equações sem intercepto foram superiores aos resultados das equações com intercepto, assim foram analisadas somente as equações sem intercepto.

A Tabela 6 apresenta os resultados obtidos para a variável selecionada. Observa-se que apenas a variável hd foi inserida no modelo, pois não houve outra variável que aumentasse o valor do R² ajustado em mais de 1%, consequentemente, foram excluídas. O modelo estimado para esta variável explica 79,07% das observações.

Tabela 6 – Resultados pelo método Stepwise Backward para o volume do tronco sem casca.

Passo	variável inserida	R^2aj	F	p-valor
1	hd	0,7907	114,31	<,0001

R²aj = coeficiente de determinação ajustado; F = valor de F para a equação, p-valor = nível de significância para F.

A Tabela 7 apresenta a variável independente selecionada com o seu parâmetro estimado e respectivo o resultado do teste t. Observa-se que variável é significativa (p<0,0001) para o modelo.

Tabela 7 – Resultado da estimativa dos parâmetros para o volume sem casca.

variável	parâmetro estimado	t	p-valor
hd	0,00076	10,69	<0,0001

t = valor de t para a equação, p-valor =  nível de significância para t.

A Tabela 8 mostra os resultados obtidos para a análise da variância para o modelo ajustado. Observa-se que o modelo ajustado é significativo (p-valor < 0,0001).

Tabela 8 – Resultado da análise da variância para o volume sem casca.

Fonte	GL	SQ	QM	F	p-valor
Modelo	1	0,00340	0,00340	114,31	<,0001
Erro	29	0,00086	0,00002
Total	30	0,00426

GL = grau de liberdade SQ = soma dos quadrados; QM = quadrado médio; F = valor de F; p-valor = nível de significância.

Após a seleção das variáveis, chegou-se ao seguinte modelo para determinar o volume do tronco sem casca::

vsc = 0,00076*hd

em que:

vsc = volume sem casca em metros cúbicos;

hd = diâmetro vezes altura.

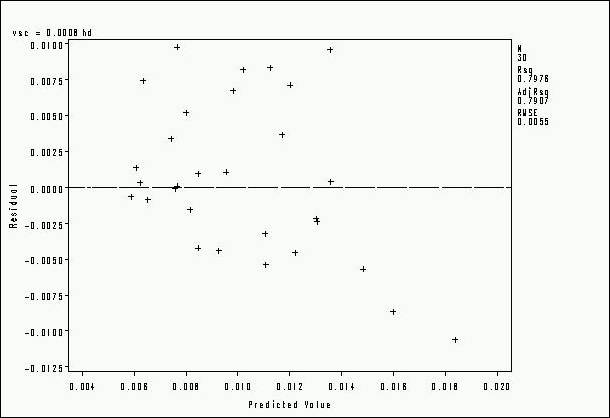
A distribuição dos resíduos do modelo ajustado para estimar o volume com casca pode ser observada na Figura 2. Pode-se observar que os resíduos do modelo ajustado são independentes e normalmente distribuídos com média zero e variância constante, o que comprova que o modelo ajustado é adequado.

Figura 2 – Distribuição dos resíduos da equação selecionada para estimar o volume sem casca.

4. CONCLUSÃO

Após o estudo realizado, verificou-se que o modelo estimado que proporcionou melhor ajuste para o volume do tronco da erva-mate com casca foi vcc = 0,01273*lnh com um R² ajustado de 75,31%. Para o volume do tronco sem casca, o modelo estimado que melhor representou essa variedade foi vsc = 0,00076*hd, com um R² ajustado de 79,07%.

Este trabalho trouxe uma importante contribuição para o estudo dessa espécie pois pode-se estimar o volume do tronco da erva-mate, tanto com casca quanto sem casca, os quais pode ser utilizado como fonte de matéria prima para diferentes fins.

BIBLIOGRAFIA

HERRMANN, M. L. P. & ROSA, O. R. Geografia do Brasil: Região Sul. Rio de Janeiro: Fundação Instituto Brasileiro de Geografia e Estatística, 1991, p. 55-84. v. 2.

LEITE, F. P. Contribuição ao conhecimento fitoecológico do Sul do Brasil. In: Fitogeografia do Sul da América. Revista Ciência e Ambiente. UFSM – Vol. 24, (janeiro/junho 2002). 152 p.

MACHADO, S. A; FIGUEIREDO FILHO, A. Dendrometria. Curitiba, 2003. 309 p.

MORENO, J. A. Clima do Rio Grande do Sul. Porto Alegre, Secretaria da Agricultura, RS, 1961. 48 p.

STRECK, E. V. et al. Solos do Rio Grande do Sul. Editora Ufrgs. 2002. p.108.

VELOSO, H. P.; RANGEL FILHO, A. L. R.; LIMA, J. C. A.. Classificação da Vegetação Brasileira, adaptada a um Sistema Universal. Rio de Janeiro: IBGE/PROJETO RADAM BRASIL, 1991. 165 p.