A FORMA DO TRONCO ATRAVÉS DA ANÁLISE DE REGRESSÃO

1. INTRODUÇÃO

A maioria dos problemas florestais, principalmente, quando se deseja obter estimativas dos parâmetros dendrométricos de florestas com baixo custo e menor tempo, normalmente utiliza-se a técnica da análise de regressão, obtendo-se através da mesma modelos matemáticos que possam ser utilizados para a estimação destes parâmetros (BRENA et al, 1978)

No Rio Grande do Sul, o Eucalyptus grandis Hill ex Maiden. é uma espécie importante para o setor madeireiro da região pelo seu desenvolvimento rápido, sendo muito utilizado nos florestamentos e reflorestamentos. Conhecendo a forma do tronco, do volume e dimensão dos seus sortimentos, o planejamento e estudo da viabilidade econômica do povoamento será facilitado.

A forma das árvores possui uma variação muito grande dentro da floresta. Essa variação ocorre, na maioria das vezes, devido à diminuição do diâmetro em direção ao topo da árvore, sendo conhecida como “taper”. Isso afeta diretamente o volume e varia conforme a espécie, a idade, o espaçamento entre árvores e as condições do sítio.

Nessa pesquisa, utiliza-se a técnica de regressão linear simples como estudo para determinar a forma do tronco das árvores, testar o modelo pré-estabelecido, definir e testar novos modelos, verificando qual o modelo matemático mais adequado para o povoamento da espécie Eucalyptus grandis Hill ex Maiden. Para isso, avaliar-se-á a equação ajustada através de testes estatísticos, permitindo conseguir uma equação com a melhor precisão possível.

2. FORMA DO TRONCO DA ÁRVORE

A árvore é constituída de quatro partes principais: raiz, tronco, fuste e copa. A parte mais importante, em termos de uso geral, é o fuste, tendo o toco e a copa sido desprezados por muito tempo. Com a escassez de madeira essas porções começaram a ganhar importância, sendo necessária a sua quantificação para uso como combustíveis e para estimar o volume de material deixado na exploração (FINGER, 1992).

O fuste, porção da árvore compreendida entre a superfície do solo (nível do solo) e a base da copa apresenta formas bastante variadas em razão do meio ambiente, da espécie, manejo, idade e de suas aptidões genéticas. Mesmo em povoamentos de uma única espécie observa-se diferentes formas entre as árvores.

As árvores da periferia, isoladas ou largamente espaçadas, sujeitas a maior intensidade de luz e, praticamente, livres de competição apresentam a forma natural, espontânea ou específica. Árvores do interior do povoamento, cuja sobrevivência se dá através da competição por água, luz e nutrientes, tendem à forma reta com pequena copa, sem ramificações laterais, conhecida como forma florestal típica.

Analisando-se uma árvore de forma típica encontra-se uma grande amplitude de variação de formas, desde as perfeitamente semelhantes a uma forma geométrica definida, até aquelas de difícil definição. Como exemplo podem ser citadas as espécies do cerrado que são tortuosas e de difícil comparação com uma forma geométrica (FINGER, 1992).

2.1. Estudo matemático das formas

Os modelos dendrométricos visam analisar a cubagem das árvores através de recursos matemáticos, comparando os sólidos geométricos de revolução às formas naturais das árvores com o objetivo de determinar seu volume. Esses sólidos são chamados de “protótipos dendrométricos” ou sólidos padrões, os quais são comparáveis com a forma do tronco ou partes deste. Os protótipos dos sólidos geométricos são obtidos pela rotação da curva geral 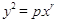ao redor do eixo x.

Para fins de estudo na Biometria Florestal considera-se: .

De acordo com o valor assumido por “r”, a forma do sólido de revolução varia, conforme exemplificado na Tabela 1. Para diferentes valores do expoente da forma “r” gera-se diferentes sólidos de revolução, como pode-se observar na Figura 1.

Tabela 1 – Variação da forma geométrica com a variação de r.

r	Designação
0	Cilindro
1	Parábola quadrática
2	Cone
3	Neilóide

Figura 1 – Sólidos de revolução de acordo com a variação do parâmetro “r”

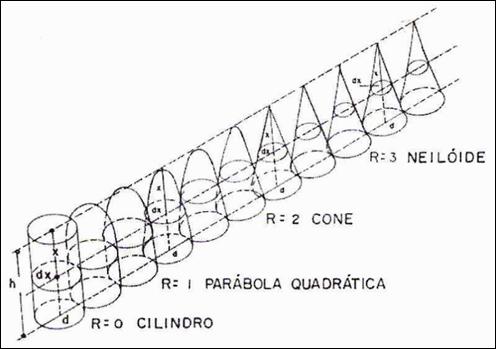
Fonte: Sterba (1986).

2.2. Forma do tronco

A forma do tronco de espécies florestais vem sendo estudada há vários anos o que é demonstrado pelo grande número de publicações encontrados na literatura técnica-científica (PEREIRA et al., 2005). Finger (1992) verificou que mesmo as árvores de forma florestal típica apresentam uma grande variação na forma do tronco, desde as formas que se assemelham a um sólido conhecido, àquelas de difícil definição.

Aliando-se certos sólidos geométricos de revolução às formas naturais das árvores, consegue-se determinar o seu volume comercial e que esses sólidos geométricos foram e são frutos de pesquisas realizadas por biometristas, numa tentativa de solucionar o problema da cubagem de árvores, através de recursos procedentes da matemática (SILVA, 1974).

Esses sólidos são obtidos pela rotação da curva geral 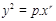ao redor do eixo “x”, onde “p” é o intercepto da equação geral. Sendo que de acordo com o valor assumido por “r” (expoente de forma), varia a forma do sólido de revolução desde um: cilindro (r=0); parábola quadrática (r=1); cone (r=2); e neilóide (r=3) (FINGER, 1992).

De acordo com Loetsch et al. (1973), um tronco não apresenta uma única forma geométrica, usando para descrevê-la o neilóide, o parabolóide e o conóide de forma associada. Husch et al. (1982) descreve o tronco de qualquer árvore como composto de vários sólidos de revolução, dividindo-o em quatro partes, entretanto acrescentam o cilindro ou hipérbole às três partes estudadas por Loetsch et al. (1973).

Hohenadl apud Silva (1974) mostrou que as árvores dominantes desenvolviam na base, maior incremento relativo em diâmetro para poderem suportar o peso do tronco. A partir desse conhecimento, várias pesquisas foram desenvolvidas para definir a forma do tronco das árvores procurando demonstrar como obter os diâmetros e os respectivos volumes a partir de alturas relativas (CAMPOS et al., 1982).

2.3. Funções de forma do tronco

As funções de forma do tronco são importantes ferramentas para prever o diâmetro em qualquer ponto do tronco a partir de uma ou mais variáveis mensuradas, onde essas funções passam a ser utilizadas também para estimar o volume do povoamento e construir tabelas de volume e sortimento para diferentes limites de dimensões de toras exigidas pelo mercado consumidor (AHRENS,1982; SCHNEIDER, 1993),

Höjer apud Figueiredo-Filho et al. (1996) foi o primeiro a fazer uma tentativa analítica para representar a forma de espécies florestais. A partir desse feito, vários métodos, modelos e formas do tronco foram testadas. Nesses processos, o computador com seus programas passou a ser uma ferramenta indispensável, estimulando o desenvolvimento de modelos mais complexos para representar a forma do tronco. O autor comenta que até meados de 1970 era muito difícil representar todo o tronco utilizando apenas uma equação. Alguns modelos eram bons, mas não descreviam todo o tronco satisfatoriamente.

No mesmo sentido Leite e Guimarães (1992) e Garcia et al. (1993) citam que os modelos matemáticos para descrever o perfil de troncos das árvores passaram a ser ferramentas importantes na obtenção de estimativas mais realísticas do volume das partes do tronco. Dentre os principais modelos empregados, incluem-se:

a) Polinomiais: Baseados na comparação entre a variável dependente (d_i/DAP)² e independente (h_i/H);

b) Sigmoidais: Utiliza-se de transformações das variáveis de modo que o modelo se assemelhe à forma natural dos troncos;

c) Segmentados: Uso de submodelos justapostos (funções spline);

d) Modelos definidos por análise multivariada: Utilização de análise multivariada para definir o modelo de regressão.

Como procedimento alternativo, Max e Burkhart (1976) utilizaram a regressão para modelar a forma do tronco. Esse método separou o tronco em três partes, as quais foram representadas por três submodelos que acrescidos de duas constantes (join points) produziram uma função de forma polinomial global e segmentada.

A técnica de modelagem empregada para descrição do perfil de troncos vem sendo utilizada com êxito e um modelo poderia ser definido como compatível ou não, quando a estimativa do volume total, obtida por integração de segmentos de tronco, seja semelhante àquela dada pela equação do volume, da qual a equação de forma foi derivada (MUNRO; DEMAERSCHALK, 1974).

A forma do tronco do Eucalyptus grandis Hill ex Maiden. foi estudada por Schneider et al. (1996) para a determinação de volume e formação de sortimentos de madeira em duas classes: serraria, com diâmetro superior a 30 cm na ponta mais fina, e indústria, para madeira com diâmetro entre 7 a 30 cm. A forma do tronco foi ajustada por um polinômio do quinto grau, tendo como variável dependente os diâmetros relativos e independente as alturas relativas 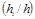, apresentando bom ajuste, boa precisão estatística, um coeficiente de determinação igual a 0,9857 e um erro padrão da estimativa de 5,14%.

3. ANÁLISE DE REGRESSÃO

A análise de regressão é utilizada para estimar um modelo estatístico que possa ser utilizado para prever os valores de uma variável dependente (Y), com base nos valores de pelo menos uma variável independente (X) (LEVINE, BERENSON, STEPHAN, 2000).

As regressões podem ser classificadas em linear e não linear, sendo que as lineares podem ser simples ou múltiplas. A regressão linear constitui um recurso estatístico da maior importância na Biometria, pois permite explicar as relações existentes entre variáveis dendrométricas como: diâmetro, altura, volume, área basal, idade, entre outras (SCHNEIDER, 1998).

O relacionamento linear entre duas variáveis é obtido pela equação 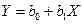(1).

(1)

onde:

X é a variável independente;

Y é a variável dependente;

b₀, b₁ são os coeficientes.

O coeficiente b₀ é definido como o intercepto e b₁ como coeficiente angular, que dá a inclinação da reta ou curva, como mostra a Figura 2.

Figura 2 – Representação de uma reta que passa pelo ponto médio ()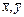

Fonte: Fonseca (1976)

Uma regressão é dita linear múltipla quando a variável dependente é explicada por duas ou mais variáveis independentes, ou seja, .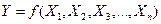

Como exemplo, pode-se citar a equação 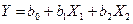(2).

(2)

Uma regressão é considerada não linear quando os coeficientes da equação encontram-se na forma de produto ou fracionária e elevados ao expoente não unitário. Como exemplo, pode-se citar as equações (3) e (4).

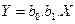(3)

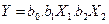(4)

As equações não lineares não têm solução pelo método dos mínimos quadrados, a não ser que possam ser linearizadas através de logaritmo.

(5)

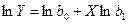(6)

A análise de regressão é composta por uma série de conjuntos de variáveis, examinando o comportamento (grandeza, média e variação) de cada variável do conjunto (Fonseca, 1976).

Essa análise é feita para que se possa encontrar alguma forma de medir a relação funcional entre as variáveis de cada conjunto, de tal forma que essa medida possa mostrar:

1) Se há relação entre as variáveis e, caso afirmativo, se é fraca ou forte;

2) Se a relação existir se estabelece um modelo que interprete a relação funcional existente entre as variáveis;

3) Constituindo o modelo, usá-lo para fim de predição. Considerando-se duas variáveis, X e Y, relacionadas por uma função matemática Y = f(X).

O diagrama de dispersão sugere a existência da relação funcional entre duas variáveis, mostrando através de uma linha construída no gráfico da Figura 3. Os pontos experimentais terão uma variação em torno da linha representativa da função, devido a existência de uma variação residual.

Figura 3 –Linha de regressão

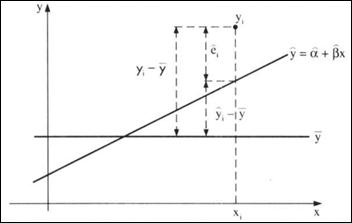
Fonte: Morettin e Bussab (2004)

3.1. Estimação dos parâmetros de regressão

Primeiramente, na análise de regressão obtém-se as estimativas “a” e “b” dos parâmetros a e b da regressão e a reta estimada. Os valores dessas estimativas serão obtidos a partir de uma amostra de n pares (x_i, y_i); i = 1, 2, 3, n.

Deseja-se que a reta seja tão próxima quanto possível do conjunto de pontos marcados, isto é, deseja-se minimizar a discrepância total entre os pontos marcados e a reta estimada. A Figura 4 ilustra tal situação:

Figura 04 – Estimação dos parâmetros

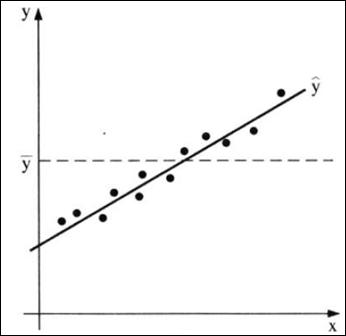
Fonte: Morettin e Bussab (2004)

3.1.1. O coeficiente de determinação R²

O coeficiente de determinação é igual à soma dos quadrados devida à regressão, dividida pela soma total dos quadrados.

(7)

O coeficiente de determinação mede a proporção da variação, que é explicada pela variável independente no modelo de regressão.

3.1.2. O coeficiente de determinação

No modelo de regressão linear simples, definimos 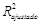como:

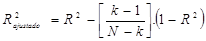(8)

onde: k = número de variáveis independentes da equação;

N = número de observações;

R² = coeficiente de determinação.

O coeficiente de determinação 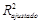é calculado para refletir tanto o número de variáveis explicativas no modelo quanto o tamanho da amostra.

3.1.3. Parâmetros de seleção do melhor modelo

Conforme Schneider (1998), para selecionar o melhor modelo para as equações de forma do tronco, podem ser utilizados os seguintes indicadores de ajuste: análise de variância, erro padrão da estimativa absoluta (S_yx), coeficiente de variação (CV), coeficiente de determinação ajustado (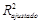) e amplitude da distribuição gráfica dos resíduos.

Neste trabalho, optou-se unicamente pelo critério de seleção do melhor modelo, ou seja o modelo que apresentar o maior coeficiente de determinação ajustado, desde que seus coeficientes sejam significativos.

4. METODOLOGIA

Para o presente estudo foram utilizados os dados referentes ao diâmetro da forma do tronco de 54 árvores disponíveis nos Relatórios de Cubagem da Empresa Aracruz Celulose S.A, no estado do Rio Grande do Sul. Inicialmente, foi utilizada a equação 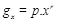que através de transformações logaritmas foi linearizada, resultando no seguinte modelo: .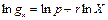

Posteriormente, a partir do parâmetro forma do tronco das árvores estudadas e analisadas pela equação 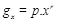será determinado esse parâmetro em função das variáveis dendrométricas (h, d). De posse dessas variáveis, elaborar-se-á várias combinações tanto para a variável dependente como para a variável independente.

Para a variável dependente, serão analisadas as seguintes combinações: r, 1/r, ln r, r² e para a variável independente as seguintes combinações: h/d, ln d, h², h²/d, d/h, d². De acordo com a significância de cada variável, serão criados modelos, para que, a partir de uma análise mais detalhada, seja selecionado o modelo mais adequado para o presente estudo. Será utilizado o coeficiente de determinação ajustado (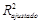) como critério para a seleção do melhor modelo. Para a análise dos dados será utilizado o Programa Statgraphics.

5. RESULTADOS

Neste trabalho, utilizou-se a análise de regressão com o objetivo do ajustamento dos dados a um modelo matemático, para a forma do tronco do Eucalyptus grandis Hill ex Maiden. A Tabela 2 mostra os resultados das cinquenta e quatro árvores estudadas que corresponde a forma do tronco das árvores (r).

Tabela 2 – Valores da forma do tronco (r) determinados pela equação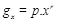

Árvore	r	Árvore	r	Árvore	r
1	1,563767	19	1,625822	37	1,350820
2	1,544262	20	1,562332	38	1,295498
3	1,849208	21	1,649325	39	1,244702
4	1,556800	22	1,429943	40	1,250472
5	1,496300	23	1,675903	41	1,163960
6	1,542291	24	1,503540	42	1,273043
7	1,595939	25	1,416741	43	1,241758
8	1,522193	26	1,337856	44	1,173776
9	1,664672	27	1,489289	45	1,250990
10	1,482515	28	1,352988	46	1,318949
11	1,525729	29	1,445189	47	1,153633
12	1,563536	30	1,271957	48	1,259647
13	1,545414	31	1,269383	49	1,273470
14	1,430281	32	1,223310	50	1,729810
15	1,574886	33	1,235987	51	1,463431
16	1,618386	34	1,268211	52	1,313493
17	1,391119	35	1,308789	53	1,336087
18	1,629260	36	1,308272	54	1,263060

Os resultados constantes da Tabela 2 mostram que os valores da forma do tronco (r) de todas as árvores estão entre 1 e 2 que correspondem a forma entre parábola quadrática e cone, conforme mencionado na Tabela 1 e apresentado na Figura 1. A Tabela 3 nos apresenta os nove modelos testados com seus respectivos coeficientes e estatísticas.

Tabela 3 – Modelos testados com seus respectivos coeficientes e estatísticas

Modelo	R²		S_yx	Coeficientes
Modelo	R²		S_yx	b₀	b₁	b₂
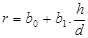
(1)	0,716569	0,711119	0,088801	2,032980	-0,463899	_____
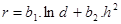
(2)	0,716638	0,691958	0,088790	_____	0,438589	- 0,000050
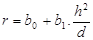
(3)	0,609471	0,601960	0,104237	2,342548	0,018022	_____
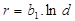
(4)	0,712360	0,693492	0,088610	_____	0,414607	_____
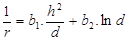
(5)	0,544382	0,516389	0,055376	_____	0,011397	0,037747
(6)	0,604498	0,596892	0,051594	0,261519	0,008828	_____
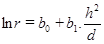
(7)	0,500674	0,491071	0,082172	0,045020	0,013316	_____
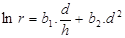
(8)	0,693415	0,668289	0,064388	_____	0,421289	-0,000006
(9)	0,703020	0,678078	0,264013	_____	-0,015878	0,834405

Todos os modelos ajustados foram significativos (p<0,05). Entretanto, utilizando-se o coeficiente de determinação ajustado (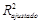) como critério para a seleção do melhor modelo, pode-se verificar que o modelo (1) 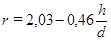apresentou o melhor resultado para o conjunto de dados que foi utilizado, onde 71,1% da variação da forma do tronco (r) é explicada pelo quociente entre a altura e o diâmetro da árvore. Os modelos (2) e (4) também apresentaram bons resultados do coeficiente de determinação ajustado, 69,1% e 69,3%, respectivamente, por outro lado, envolvem cálculos com logaritmos, sendo, portanto, não selecionados pelo princípio da parcimônia. Os modelos (5) e (6) apresentaram os menores erro padrão da estimativa absoluta (S_yx), porém também apresentaram valores mais baixos de coeficiente de determinação ajustado. Os demais modelos apresentaram valores menores de coeficiente de determinação ajustado, entre 67,8% e 49,1%.

6. CONCLUSÃO

O estudo mostrou que a forma das árvores possui uma variação muito grande dentro da floresta (cilindro, parábola quadrática, cone e neilóide) e essa variação ocorre, na maioria das vezes, devido à diminuição do diâmetro em direção ao topo da árvore, afetando diretamente o volume e variando com a espécie, idade, espaçamento entre árvores e condições de sítio, o que vem a corroborar com a literatura.

Foram encontrados nove modelos para analisar a forma do tronco da espécie estudada, através da metodologia da análise de regressão que não geraram os mesmos resultados, embora baseados no mesmo conjunto de dados. O modelo 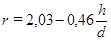foi o que melhor coeficiente de determinação ajustado (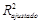), sendo, portanto, o modelo mais adequado encontrado para modelar a forma do tronco das árvores d a espécie Eucalyptus grandis Hill ex Maiden, no estado do Rio Grande do Sul , do Brasil.

A contribuição do presente estudo esta no fato de que com apenas duas variáveis dendrométricas medidas a campo (diâmetro e altura ) é possível determinar a forma do tronco das árvores de uma maneira rápida e eficiente.

REFERÊNCIAS

AHRENS S. Análise de componentes principais e a simulação da forma do tronco. In: Seminário sobre atualidades e perspectivas florestais: o uso de funções de forma de tronco em estudos de volumetria de espécies florestais, 5., 1982, Curitiba. Curitiba: EMBRAPA, URPFCS, 1982. p. 77–92.

BRENA DA, SILVA JNM, SCHINEIDER PR. Metodologia para verificação das condicionantes da análise de regressão. Revista Floresta, 1978, 9(2):25-45.

CAMPOS JCC, ZUCONI JM, RIBEIRO, JC. Teste de um novo modelo para expressar “taper”. In: Seminário sobre atualidades e perspectivas florestais: o uso de funções de forma de tronco em estudos de volumetria de espécies florestais, 5., 1982, Curitiba. Curitiba: EMBRAPA, URPFCS, 1982. p. 47–50.

DRESCHER R, SCHNEIDER PR, FINGER CAG. Sortimentos de Pinus elliottii Engelm para a região da serra do sudeste do Estado do Rio Grande do Sul - Brasil. Ciência Florestal, Santa Maria. 1999, 9(2),55-73.

FIGUEIREDO-FILHO A, BORDERS BE, HITCH, KL. Taper equations for Pinus taeda L. plantations in Southern Brazil. Forest Ecology and Management. 1996,1(83):39-46.

FINGER CAG. Fundamentos de biometria florestal. Santa Maria: UFSM, CEPEF-FATEC, 1992. 269 p.

FONSECA JS. MARTINS GA, TOLEDO GL. Estatística aplicada. São Paulo: Atlas, 1976. 273 p.

GARCIA SLR, LEITE HG, YARED JAG. Análise do perfil do tronco de Morototó (Didymopanax morotototoni) em função do espaçamento. In: Congresso florestal panamericano, 1., congresso florestal brasileiro, 7., 1993, Curitiba. Curitiba: SBS/SBEF, 1993. p. 485–491.

HUSCH B, MILLER IC, BEERS TW. Forest mensuration. New York: J. Wiley, 1982. 402 p.

LEITE HG, GUIMARÃES DP. Um novo modelo para descrever o perfil do tronco. Revista Árvore, Viçosa – MG 1992,2(16): 170-180.

LEVINE DM, BERENSON ML, STEPHAN, D. Estatística: teoria e aplicações usando Microsoft Excel em português. Rio de Janeiro: LTC, 2000.

LOETSCH F, ZOEHRER F, HALLER KE. Forest inventory. München: BLV, 1973. 469 p. v. 2.

MAX TA, BURKHART HE. Segmented polinomial regression applied to taper equations. For. Sci. 1976,33(22): 283–289.

MORETTIN PA, BUSSAB WO. Estatística Básica. 5ª edição. São Paulo: Saraiva, 2004.

MUNRO DD, DEMAERSCHALK J. Taper-based versus volume based compatible estimating systems. For. Chron., 1974,5(50):197–199.

PEREIRA JES, ANSUJ AP, MULLER I, AMADOR J. Modelagem do volume do tronco do Eucalyptus grandis Hill ex Maiden. In: XII Simpósio de Engenharia de Produção - SIMPEP, 2005, Bauru. Anais ... Bauru: DEP/UNESP, 2005.

SCHNEIDER PR. Introdução ao manejo florestal. Santa Maria – UFSM/CEPEF-FATEC, 1993. 348 p.

SCHNEIDER PR, FINGER CAG, KLEIN JEM. Forma de tronco e sortimentos de madeira de Eucalyptus grandis Maiden. para o Estado do Rio Grande do Sul. Ciência Florestal, Santa Maria, 1996,1(7):85-91.

SCHNEIDER PR. Análise de regressão aplicada à Engenharia Florestal. Santa Maria- UFSM/CEPEF, 1998. 236 p.

SILVA JA. Seleção de parcelas amostrais aplicadas em povoamentos de Pinus taeda L. para fins biométricos em Santa Maria – RS. 1974. 87 p. Dissertação (Mestrado em Engenharia Rural) – Universidade Federal de Santa Maria, Santa Maria, 1974.

STERBA H. Holzmeßlehre. Wiew: Univ. für Bodenkultur. 1986. 169 p.

RESUMO

ABSTRACT